摘要：27(7).如图所示.已知双曲线y=与直线y=x相交于A.B两点．第一象限上的点M是双曲线y=上的动点．过点B作BD∥y轴交x轴于点D．过N作NC∥x轴交双曲线y=于点E.交BD于点C． .求A.B两点的坐标及k的值,(2)若B是CD的中点.四边形OBCE的面积为4.求直线CM的解析式,(3)设直线AM.BM分别与y轴相交于P.Q两点.且MA=pMP.MB=qMQ.求p-q的值．
网址：http://m.1010jiajiao.com/timu_id_156647[举报]
如图所示的是蜂巢的一部分，从中间阴影算起，有27层，每个正六边形的小室中放进一个幼蜂，那么这个蜂巢总计可以放多少只幼蜂？
如图所示的是某月的日历，带阴影的方框中的9个数中，最中间的数设为x，请用含x的式子表示出中间数的左上方的数与右下方的数，试问这三个数的和可能是27吗？为什么？28呢？
2、如图所示，AB∥CD，∠E=27°，∠C=52°，则∠EAB的度数为（ ）小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是（ ）
| A、12分钟 | B、15分钟 | C、25分钟 | D、27分钟 |
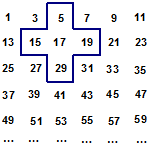将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．探究规律一：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为
结论：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是
探究规律二：
落在十字框中间且又是第二列的奇数是15，27，39…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列，第五列的奇数分别可表示为
运用规律：
（1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是
（2）请你写出一个不能够框在十字框中间的且大于500的奇数：
（3）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．
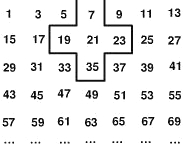
变通运用：
若把这些奇数重新排列如右图，解答下列问题：
（1）下列能被十字框框在中间的奇数是（
A.841 B.1121 C.1263 D.1091
（2）被框在十字框中的五个数之和可能是1925吗？说说你的理由． 查看习题详情和答案>>