摘要：那么当n=k+1时,设第k+1个圆为⊙O,由题意,它与k个圆中每个圆交于两点,又无三个圆交于同一点,于是它与其他k个圆交于2k个点,这些点把⊙O分成2k条弧,即f+2k=k2-k+2+2k=(k+1)2-(k+1)+2. 6分这就是说,当n=k+1时,命题也成立.综上可知,对一切n∈N*,命题都成立. 8分
网址：http://m.1010jiajiao.com/timu_id_15448[举报]
设数列{an}满足a1=2,an+1=2an+2,用数学归纳法证明an=4×2n-1-2的第二步中,设n=k时结论成立,即ak=4×2k-1-2,那么当n=k+1时, __________.
查看习题详情和答案>>
某同学回答“用数学归纳法证明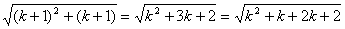
＜n+1(n∈N)”的过程如下:
＜n+1(n∈N)”的过程如下:证明：(1)当n=1时,显然命题是正确的;(2)假设n=k时有
＜k+1,那么当n=k+1时,
=(k+1)+1,所以当n=k+1时命题是正确的,由(1)(2)可知对于n∈N,命题都是正确的.以上证法是错误的,错误在于( )
A.当n=1时,验证过程不具体
B.归纳假设的写法不正确
C.从k到k+1的推理不严密
D.从k到k+1的推理过程没有使用归纳假设
查看习题详情和答案>>数列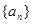
，满足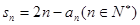
（1）求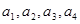
，并猜想通项公式
。
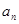（2）用数学归纳法证明（1）中的猜想。
【解析】本试题主要考查了数列的通项公式求解，并用数学归纳法加以证明。第一问利用递推关系式得到
，
，
，
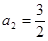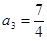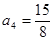，并猜想通项公式
第二问中，用数学归纳法证明（1）中的猜想。
①对n=1，等式成立。
②假设n=k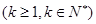
时，
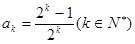成立，
那么当n=k+1时，
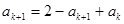，所以当n=k+1时结论成立可证。
数列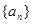，满足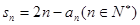
（1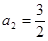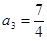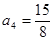），，，并猜想通项公。 …4分
（2）用数学归纳法证明（1）中的猜想。①对n=1，等式成立。 …5分
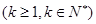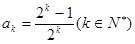②假设n=k时，成立，
那么当n=k+1时，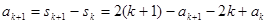
，
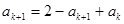……9分
所以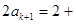
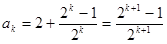
所以当n=k+1时结论成立 ……11分
由①②知，猜想对一切自然数n均成立
查看习题详情和答案>>