摘要:平面内有n个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:n个圆把平面分成f(n)=n2-n+2个部分.分析 本题的关键在于如何应用归纳假设及已知条件分析当n=k+1时,第k+1个圆与其他k个圆的交点个数,做到有目的的变形.证明 (1)当n=1时,一个圆把平面分成两部分,又12-1+2=2,故命题成立.时,命题成立,即满足题设条件的k个圆把平面分成f(k)=k2-k+2个部分.2分
网址:http://m.1010jiajiao.com/timu_id_15447[举报]
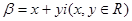 与复平面上点P(x,y)对应,且复数
与复平面上点P(x,y)对应,且复数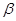 满足条件
满足条件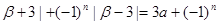 a(其中n
a(其中n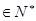 .常数a
.常数a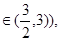 当n为奇数时,动点P(x,y)的轨迹为C1,
当n为偶数时,动点P(x,y)的轨迹为C2,且两条曲线都经过点D(2,
当n为奇数时,动点P(x,y)的轨迹为C1,
当n为偶数时,动点P(x,y)的轨迹为C2,且两条曲线都经过点D(2,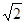 ),求轨迹C1 与C2的方程?
),求轨迹C1 与C2的方程?