摘要:由已知得:
网址:http://m.1010jiajiao.com/timu_id_154334[举报]
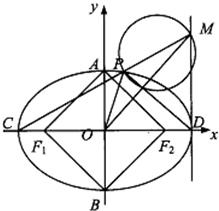 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明:
| OM |
| OP |
(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由. 查看习题详情和答案>>
已知函数f(x)=ax+b
(x≥0),且函数f(x)与g(x)的图象关于直线y=x对称,又f(
)=2-
,g(1)=0.
(Ⅰ)求f(x)的值域;
(Ⅱ)是否存在实数m,使得命题p:f(m2-m)<f(3m-4)和q:g(
)>
满足复合命题p且q为真命题?若存在,求出m的取值范围;若不存在,说明理由.
查看习题详情和答案>>
| 1+x2 |
| 3 |
| 3 |
(Ⅰ)求f(x)的值域;
(Ⅱ)是否存在实数m,使得命题p:f(m2-m)<f(3m-4)和q:g(
| m-1 |
| 4 |
| 3 |
| 4 |
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e]时,f(x)=ax+lnx(其中e是自然界对数的底,a∈R)
(1)求f(x)的解析式;
(2)设g(x)=
,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+
;
(3)是否存在实数a,使得当x∈[-e,0)时,f(x)的最小值是3?如果存在,求出实数a的值;如果不存在,请说明理由. 查看习题详情和答案>>
(1)求f(x)的解析式;
(2)设g(x)=
| ln|x| |
| |x| |
| 1 |
| 2 |
(3)是否存在实数a,使得当x∈[-e,0)时,f(x)的最小值是3?如果存在,求出实数a的值;如果不存在,请说明理由. 查看习题详情和答案>>