摘要:解法一 ∵()n=0,∴||<1
网址:http://m.1010jiajiao.com/timu_id_15429[举报]
下列说法正确的是:
①?x∈N+,(x-1)2>0 ②
•
=
•
,则
=
③函数f(x)=sinx在第一象限内是增函数.
④“m<
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是
查看习题详情和答案>>
①?x∈N+,(x-1)2>0 ②
| a |
| b |
| a |
| c |
| b |
| c |
③函数f(x)=sinx在第一象限内是增函数.
④“m<
| 1 |
| 4 |
⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是
④⑤
④⑤
.
下列说法正确的是:
①?x∈N+,(x-1)2>0 ②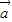 •
•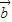 =
=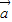 •
•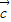 ,则
,则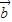 =
=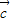
③函数f(x)=sinx在第一象限内是增函数.
④“m< ”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是 . 查看习题详情和答案>>
①?x∈N+,(x-1)2>0 ②
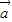 •
•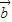 =
=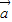 •
•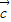 ,则
,则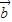 =
=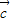
③函数f(x)=sinx在第一象限内是增函数.
④“m<
 ”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是 . 查看习题详情和答案>>
下列说法正确的是:
①?x∈N+,(x-1)2>0 ②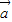 •
•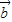 =
=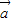 •
•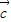 ,则
,则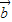 =
=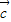
③函数f(x)=sinx在第一象限内是增函数.
④“m< ”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是 . 查看习题详情和答案>>
①?x∈N+,(x-1)2>0 ②
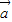 •
•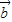 =
=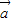 •
•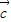 ,则
,则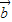 =
=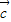
③函数f(x)=sinx在第一象限内是增函数.
④“m<
 ”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.⑤函数f(x)=2x+3x的零点所在的一个区间是(-1,0).其中正确的序号是 . 查看习题详情和答案>>
已知二次函数f(x)=ax2+bx+3是偶函数,且过点(-1,4),函数g(x)=x+4.
(1)求f(x)的解析式;
(2)求函数y=f(2x)+g(2x+1)的值域;
(3)定义在[p,q]上的一个函数m(x),用分法T:p=x0<x1<…<xi-1<xi<…<xn=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得不等式|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xi)-m(xi-1)|+…+|m(xn)-m(xn-1)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数.试判断函数f(x)是否为在[1,2]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.
查看习题详情和答案>>
(1)求f(x)的解析式;
(2)求函数y=f(2x)+g(2x+1)的值域;
(3)定义在[p,q]上的一个函数m(x),用分法T:p=x0<x1<…<xi-1<xi<…<xn=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得不等式|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xi)-m(xi-1)|+…+|m(xn)-m(xn-1)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数.试判断函数f(x)是否为在[1,2]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.
在平面直角坐标系中,已知O为坐标原点,点A的坐标为(a,b),点B的坐标为(cosωx,sinωx),其中a2+b2≠0且ω>0.设f(x)=
•
.
(1)若a=
,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;
(2)若点A是过点(-1,1)且法向量为
=(-1,1)的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;
(3)根据本题条件我们可以知道,函数f(x)的性质取决于变量a、b和ω的值.当x∈R时,试写出一个条件,使得函数f(x)满足“图象关于点(
,0)对称,且在x=
处f(x)取得最小值”.
查看习题详情和答案>>
| OA |
| OB |
(1)若a=
| 3 |
(2)若点A是过点(-1,1)且法向量为
| n |
(3)根据本题条件我们可以知道,函数f(x)的性质取决于变量a、b和ω的值.当x∈R时,试写出一个条件,使得函数f(x)满足“图象关于点(
| π |
| 3 |
| π |
| 6 |