摘要：∴Sn=a1+a2+-+an=2(1-+-+-+-)=.
网址：http://m.1010jiajiao.com/timu_id_15407[举报]
已知Sn=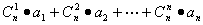
a1+
a2+…+
an,n∈N*.
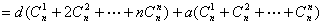a1+a2+…+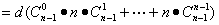an,n∈N*.(1)若Sn=n·2n-1(n∈N*),是否存在等差数列{an}对一切自然数n满足上述等式?
(2)若数列{an}是公比为q(q≠±1),首项为1的等比数列,b1+b2+…+bn=
(n∈N*).求证:{bn}是等比数列.
{an}是正项数列，其前n项．和为Sn，且1与Sn的几何平均数等于1与an的算术平均数．
（1）求证：{an}为等差数列，并求an
（2）若
+
+…+
＜logm2（m2-m）关于n∈N*恒成立，求正数m的范围；
（3）记Tn=
+
+…+
，求证：4T2n≥n+2．
查看习题详情和答案>>
（1）求证：{an}为等差数列，并求an
（2）若
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
（3）记Tn=
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
(1)
(
-an-b)=0,求实数a、b的值;
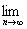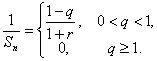(-an-b)=0,求实数a、b的值;(2)已知数列{an}满足条件a1=1,a2=r(r＞0),且{an·an+1}是公比为q(q＞0)的等比数列,bn=a2n-1+a2n(n=1,2,…).求bn和
,其中Sn=b1+b2+…+bn.
，a2＋a5＝4，an＝33，试求n的值．