摘要：令f′(t)=-t2+=0,得t=,t=-.
网址：http://m.1010jiajiao.com/timu_id_15291[举报]
已知函数f（x）定义在区间（-1，1）上，f（
）=-1，且当x，y∈（-1，1）时，恒有f（x）-f（y）=f（
），又数列{an}满足：a1=
，an+1=
．
（I）证明：f（x）在（-1，1）上为奇函数；
（II）求f（an）关于n的函数解析式；
（III）令g（n）=f（an）且数列{an}满足bn=
，若对于任意n∈N+，都有b1+b2+…+bn＜t2-3t恒成立，求实数t的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2an | ||
1+
|
（I）证明：f（x）在（-1，1）上为奇函数；
（II）求f（an）关于n的函数解析式；
（III）令g（n）=f（an）且数列{an}满足bn=
| 1 |
| g(n) |
已知在数列{an}中，a1=t，a2=t2，其中t＞0，x=
是函数f（x）=an-1x3-3[（t+1）an-an+1]x+1（n≥2）的一个极值点
（Ⅰ）求数列{an}的通项公式
（Ⅱ）当t=2时，令bn=
，数列{bn}前n项的和为Sn，求证：Sn＜
（Ⅲ）设cn=
，数列{cn}前n项的和为Tn，求同时满足下列两个条件的t的值：
（1）Tn＜
（2）对于任意的m∈(0，
)，均存在k∈N*，当n≥k时，Tn＞m．
查看习题详情和答案>>
| t |
（Ⅰ）求数列{an}的通项公式
（Ⅱ）当t=2时，令bn=
| an-1 |
| (an+1)(an+1+1) |
| 1 |
| 6 |
（Ⅲ）设cn=
| 1 |
| 2 |
| an |
| (2n+1)(2n+1+1) |
（1）Tn＜
| 1 |
| 6 |
（2）对于任意的m∈(0，
| 1 |
| 6 |
（14分）已知在数列｛an｝中，a1=t，a2=t2，其中t>0，x=
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点（Ⅰ）求数列｛an｝的通项公式
（Ⅱ）当
时，令
，数列
前
项的和为
，求证：
（Ⅲ）设
，数列
前项的和为
，
求同时满足下列两个条件的
的值：（1）
（2）对于任意的
，均存在
，当
时，
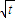是函数f（x）=an-1x3-3[（t+1）an-an+1]x+1（n≥2）的一个极值点
，数列{bn}前n项的和为Sn，求证：Sn
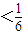
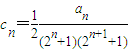，数列{cn}前n项的和为Tn，求同时满足下列两个条件的t的值：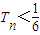
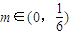，均存在k∈N*，当n≥k时，Tn＞m．
=1按向量a=(t-3,t2)(t∈R)平移后得到曲线E,设曲线E的右焦点为P.
),且
(m∈R),求∠AOB(O为坐标原点)的最大值.