题目内容
已知椭圆(1)求P点轨迹C的方程;
(2)A、B为曲线C上的两点,F(0,![]() ),且
),且![]() (m∈R),求∠AOB(O为坐标原点)的最大值.
(m∈R),求∠AOB(O为坐标原点)的最大值.
(文)已知函数f(x)=xn+1(n∈N*,x≠0).
(1)讨论函数f(x)图象的对称性,并指出其一条对称轴或一个对称中心;
(2)令an=f′(x),求数列{an}的前n项和Sn.
答案:解:(1)设平移后的右焦点为P(x,y),易得已知椭圆的右焦点为F1(3,0),
则![]() +a=
+a=![]() ,即(3,0)+(t-3,t2)=(x,y),∴
,即(3,0)+(t-3,t2)=(x,y),∴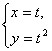 (t∈R),即轨迹C的方程为y=x2.
(t∈R),即轨迹C的方程为y=x2.
(2)易知F(0,![]() )为曲线C的焦点,又AF=mBF(m∈R).
)为曲线C的焦点,又AF=mBF(m∈R).
设A(x1,x12),B(x2,x22),其中x1>0,x2<0.则kOA=![]() =x1,kOB=
=x1,kOB=![]() =x2.
=x2.
∴tan∠AOB=![]() .?设直线AB的方程为y=kx+
.?设直线AB的方程为y=kx+![]() ,代入y=x2,得x2-kx-
,代入y=x2,得x2-kx-![]() =0,
=0,
∴x2x1=-![]() ,
,
代入?得tan∠AOB=![]() =
=![]() (x2-x1)=-
(x2-x1)=-![]() (x1-x2)≤-
(x1-x2)≤-![]() ×2
×2![]()
=-![]() (当且仅当AB∥x轴时取等号).
(当且仅当AB∥x轴时取等号).
∴∠AOB≤π-arctan![]() ,即∠AOB的最大值为π-arctan
,即∠AOB的最大值为π-arctan![]() .
.
(文)解:(1)当n为偶数时,因为f(-x)=(-x)n+1=xn+1=f(x),即函数f(x)为偶函数,所以其图象关于y轴对称.2分
当n为奇数时,因为f(-x)=(-x)n+1=-xn+1,所以![]() =1.
=1.
所以其图象关于点(0,1)中心对称.
〔或令g(x)=f(x)-1=xn,所以g(-x)=(-x)n=-xn=-g(x),即g(x)为奇函数.
所以g(x)的图象关于原点对称,故函数f(x)的图象关于点(0,1)中心对称〕
(2)an=f′(x)=nxn-1,6分所以Sn=1+2x+3x2+…+nxn-1.#当x=1时,Sn=![]() ;
;
当x≠1时,#式两边同乘x,得xSn=x+2x2+3x3+…+(n-1)xn-1+nxn.?
?式-#式可得Sn=![]() .
.

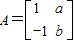 ,A的一个特征值λ=2,其对应的特征向量是
,A的一个特征值λ=2,其对应的特征向量是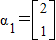 .
.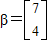 ,计算A2β的值.
,计算A2β的值.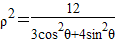 ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为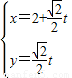 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和.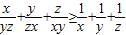 .
.