摘要:综合以上得.------------------13分
网址:http://m.1010jiajiao.com/timu_id_151923[举报]
(09年山东省实验中学综合测试理)(本小题满分13分)已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线![]() 是抛物线
是抛物线![]() 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)过点![]() 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一
的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一
个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,
请说明理由.
查看习题详情和答案>>已知函数 .(
.( )
)
(1)若 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
【解析】第一问中,首先利用 在区间
在区间 上单调递增,则
上单调递增,则 在区间
在区间 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间 上单调递增,
上单调递增,
则 在区间
在区间 上恒成立. …………3分
上恒成立. …………3分
即 ,而当
,而当 时,
时, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令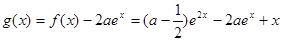 ,定义域为
,定义域为 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,
,
当 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有 ,不合题意;
,不合题意;
当 ,即
,即 时,同理可知,
时,同理可知, 在区间
在区间 上递增,
上递增,
有 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若 ,则有
,则有 ,此时在区间
,此时在区间 上恒有
上恒有 ,从而
,从而 在区间
在区间 上是减函数;
上是减函数;
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是
的范围是 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
查看习题详情和答案>>