网址:http://m.1010jiajiao.com/timu_id_150799[举报]
一、
1.C 2.A 3.D 4.C 5.A 6.B 7.A 8.C 9.D 10.C
11.D 12.B
1~5略
6.理科数学.files/image213.gif) 或
或理科数学.files/image215.gif) .
.
7.解:理科数学.files/image062.gif)
理科数学.files/image218.gif)
理科数学.files/image220.gif) .
.
其展开式中含理科数学.files/image028.gif) 的项是:
的项是:理科数学.files/image223.gif) ,系数等于
,系数等于理科数学.files/image008.gif) .
.
8.解:根据题意:理科数学.files/image226.gif) .
.
9.解:理科数学.files/image228.gif) ,椭圆离心率为
,椭圆离心率为理科数学.files/image230.gif) ,
,理科数学.files/image232.gif) ,
,理科数学.files/image234.gif) .
.
10.解:依腰意作出图形.取理科数学.files/image236.gif) 中点
中点理科数学.files/image238.gif) ,连接
,连接理科数学.files/image240.gif) 、
、理科数学.files/image242.gif) ,则
,则理科数学.files/image244.gif) ,不妨设四面体棱长为2,则
,不妨设四面体棱长为2,则理科数学.files/image246.gif) 是等腰三角形,
是等腰三角形,理科数学.files/image248.gif) 必是锐角,
必是锐角,理科数学.files/image248.gif) 就是
就是理科数学.files/image100.gif) 与
与理科数学.files/image102.gif) 所成的角,
所成的角,理科数学.files/image252.gif) .
.
理科数学.files/image253.jpg)
11.解:已知两腰所在直线斜率为1,理科数学.files/image255.gif) ,设底边所在直线斜率为
,设底边所在直线斜率为理科数学.files/image210.gif) ,已知底角相等,由到角公式得:
,已知底角相等,由到角公式得:
理科数学.files/image258.jpg)
理科数学.files/image260.gif) ,解得
,解得理科数学.files/image262.gif) 或
或理科数学.files/image121.gif) .
.
由于等腰三角底边过点(理科数学.files/image116.gif) ,0)则只能取
,0)则只能取理科数学.files/image266.gif) .
.
12.解:如图,正四面体理科数学.files/image094.gif) 中,
中,理科数学.files/image269.gif) 是
是
理科数学.files/image271.jpg)
理科数学.files/image273.gif) 中心,连
中心,连理科数学.files/image275.gif) ,此四面体内切球与外接球具有共同球心
,此四面体内切球与外接球具有共同球心理科数学.files/image277.gif) .
.理科数学.files/image277.gif) 必在
必在理科数学.files/image275.gif) 上,并且
上,并且理科数学.files/image281.gif) 等于内切球半径,
等于内切球半径,理科数学.files/image283.gif) 等于外接球半径.记
等于外接球半径.记理科数学.files/image285.gif) 面积为
面积为理科数学.files/image287.gif) ,则
,则理科数学.files/image289.gif)
理科数学.files/image291.gif) ,从而
,从而理科数学.files/image293.gif) .
.
二、
13.理科数学.files/image295.gif) .解:
.解:理科数学.files/image297.gif) ,
,理科数学.files/image299.gif) 与
与理科数学.files/image125.gif) 共线
共线理科数学.files/image302.gif) .
.
14.理科数学.files/image304.gif) .解:
.解:理科数学.files/image306.gif) ,曲线
,曲线理科数学.files/image129.gif) 在(1,0)处的切线与直线
在(1,0)处的切线与直线理科数学.files/image133.gif) 垂直,则
垂直,则理科数学.files/image310.gif) ,
,理科数学.files/image133.gif) 的倾角是
的倾角是理科数学.files/image304.gif) .
.
15.曲线理科数学.files/image135.gif) ①,化作标准形式为
①,化作标准形式为理科数学.files/image315.gif) ,表示椭圆,由于对称性.取焦点
,表示椭圆,由于对称性.取焦点理科数学.files/image317.gif) ,过
,过理科数学.files/image238.gif) 且倾角是135°的弦所在直线方程为:
且倾角是135°的弦所在直线方程为:理科数学.files/image320.gif) ,即
,即理科数学.files/image322.gif) ②,联立式①与式②.消去y,得:
②,联立式①与式②.消去y,得:理科数学.files/image324.gif) ,由弦长公式得:
,由弦长公式得:理科数学.files/image326.gif) .
.
16.充要条件①:底面是正三角形,顶点在底面的射影恰是底面的中心.
充要条件②:底面是正三角形.且三条侧棱长相等,
充要条件③:底面是正三角形,且三个侧面与底面所成角相等.
再如:底面是正三角形.且三条侧棱与底面所成角相等;三条侧棱长相等,且三个侧面与底面所成角相等;三个侧面与底面所成角相等,三个侧面两两所成二面角相等.
三、
17.解:理科数学.files/image328.gif) ,则
,则理科数学.files/image330.gif) ,
,理科数学.files/image332.gif) ,
,理科数学.files/image334.gif) .由正弦定理得
.由正弦定理得
理科数学.files/image336.gif) ,
,
理科数学.files/image338.gif)
理科数学.files/image340.gif) .
.
18.(1)证:已知理科数学.files/image145.gif) 是正三棱柱,取
是正三棱柱,取理科数学.files/image098.gif) 中点
中点理科数学.files/image277.gif) ,
,理科数学.files/image345.gif) 中点
中点理科数学.files/image238.gif) ,连
,连理科数学.files/image348.gif) ,
,理科数学.files/image350.gif) ,则
,则理科数学.files/image350.gif) 、
、理科数学.files/image352.gif) 、
、理科数学.files/image348.gif) 两两垂直,以
两两垂直,以理科数学.files/image350.gif) 、
、理科数学.files/image352.gif) 、
、理科数学.files/image348.gif) 为
为理科数学.files/image028.gif) 、
、理科数学.files/image030.gif) 、
、理科数学.files/image357.gif) 轴建立空间直角坐标系,又已知
轴建立空间直角坐标系,又已知理科数学.files/image359.gif) ,
,
则理科数学.files/image361.gif)
理科数学.files/image363.gif) .
.
理科数学.files/image365.gif) ,
,理科数学.files/image367.gif) ,则
,则理科数学.files/image369.gif) ,又因
,又因理科数学.files/image371.gif) 与
与理科数学.files/image373.gif) 相交,故
相交,故理科数学.files/image375.gif) 面
面理科数学.files/image160.gif) .
.
(2)解:由(1)知,理科数学.files/image378.gif) 是面
是面理科数学.files/image160.gif) 的一个法向量.
的一个法向量.
理科数学.files/image381.jpg)
理科数学.files/image383.gif) ,设
,设理科数学.files/image385.gif) 是面
是面理科数学.files/image387.gif) 的一个法向量,则
的一个法向量,则理科数学.files/image389.gif) ①,
①,理科数学.files/image391.gif) ②,取
②,取理科数学.files/image393.gif) ,联立式①、②解得
,联立式①、②解得理科数学.files/image395.gif) ,则
,则理科数学.files/image397.gif) .
.
二面角理科数学.files/image162.gif) 是锐二面角,记其大小为
是锐二面角,记其大小为理科数学.files/image400.gif) .则
.则
理科数学.files/image402.gif) ,
,
二面角理科数学.files/image162.gif) 的大小
的大小理科数学.files/image405.gif) ,亦可用传统方法解(略).
,亦可用传统方法解(略).
19.解:已知各投保学生是否出险相互独立,且每个投保学生在一年内出险的概率都是理科数学.files/image407.gif) ,记投保的5000个学生中出险的人数为
,记投保的5000个学生中出险的人数为理科数学.files/image409.gif) ,则
,则理科数学.files/image411.gif) (5000,0.004)即
(5000,0.004)即理科数学.files/image409.gif) 服从二项分布.
服从二项分布.
(1)记“保险公司在学平险险种中一年内支付赔偿金至少5000元”为事件A,则
理科数学.files/image414.gif) ,
,
理科数学.files/image416.gif) .
.
(2)该保险公司学平险除种总收入为理科数学.files/image418.gif) 元=25万元,支出成本8万元,支付赔偿金5000
元=25万元,支出成本8万元,支付赔偿金5000理科数学.files/image409.gif) 元=0.5
元=0.5理科数学.files/image409.gif) 万元,盈利
万元,盈利理科数学.files/image421.gif) 万元.
万元.
由理科数学.files/image409.gif) ~
~理科数学.files/image424.gif) 知,
知,理科数学.files/image426.gif) ,
,
进而理科数学.files/image428.gif) 万元.
万元.
故该保险公司在学平险险种上盈利的期望是7万元.
20.解(1):由理科数学.files/image430.gif) 得
得理科数学.files/image432.gif) ,即
,即理科数学.files/image434.gif) ,
,
理科数学.files/image436.gif) ,而
,而理科数学.files/image174.gif)
理科数学.files/image439.jpg)
由表可知,理科数学.files/image072.gif) 在
在理科数学.files/image442.gif) 及
及理科数学.files/image444.gif) 上分别是增函数,在
上分别是增函数,在理科数学.files/image446.gif) 及
及理科数学.files/image448.gif) 上分别是减函数.
上分别是减函数.
理科数学.files/image450.gif) .
.
(2)理科数学.files/image452.gif) 时,
时,理科数学.files/image186.gif) 等价于
等价于理科数学.files/image455.gif) ,记
,记理科数学.files/image457.gif) ,
,
则理科数学.files/image459.gif) ,因
,因理科数学.files/image461.gif) ,
,
则理科数学.files/image463.gif) 在
在理科数学.files/image465.gif) 上是减函数,
上是减函数,理科数学.files/image467.gif) ,故
,故理科数学.files/image469.gif) .
.
当理科数学.files/image471.gif) 时,
时,理科数学.files/image473.gif) 就是
就是理科数学.files/image475.gif) ,显然成立,综上可得
,显然成立,综上可得理科数学.files/image188.gif) 的取值范围是:
的取值范围是:理科数学.files/image478.gif)
22.解:(1)由条件可知椭圆的方程是:
理科数学.files/image480.jpg)
理科数学.files/image482.gif) ①,直线
①,直线理科数学.files/image194.gif) 的方程是
的方程是理科数学.files/image485.gif) ②,
②,
联立式①、②消去理科数学.files/image030.gif) 并整理得
并整理得理科数学.files/image488.gif) ,由此出发时,
,由此出发时,理科数学.files/image490.gif) 是等比数列,
是等比数列,
理科数学.files/image492.gif) .
.
(2)由(1)可知,理科数学.files/image494.gif) .当
.当理科数学.files/image496.gif) 时,
时,
理科数学.files/image498.gif)
理科数学.files/image500.gif) ,
,
理科数学.files/image166.gif) 是递减数列
是递减数列理科数学.files/image503.gif)
对理科数学.files/image496.gif) 恒成立
恒成立理科数学.files/image506.gif) .
.
理科数学.files/image508.gif) ,
,理科数学.files/image510.gif) 时,
时,理科数学.files/image166.gif) 是递减数列.
是递减数列.
21.解(1):理科数学.files/image181.gif) ,由
,由理科数学.files/image514.gif) 解得函数定义域呈
解得函数定义域呈理科数学.files/image516.gif) .
.
理科数学.files/image518.gif) ,由
,由理科数学.files/image520.gif) 解得
解得理科数学.files/image522.gif) ,列表如下:
,列表如下:
理科数学.files/image028.gif)
理科数学.files/image442.gif)
理科数学.files/image526.gif)
理科数学.files/image528.gif)
理科数学.files/image530.gif)
理科数学.files/image532.gif)
理科数学.files/image444.gif)
理科数学.files/image535.gif)
理科数学.files/image537.gif)
0
理科数学.files/image539.gif)
理科数学.files/image539.gif)
0
理科数学.files/image537.gif)
理科数学.files/image072.gif)
ㄊ
极大
ㄋ
ㄋ
极小
ㄊ
解得理科数学.files/image542.gif) ,进而求得
,进而求得理科数学.files/image098.gif) 中点
中点理科数学.files/image545.gif) .
.
己知理科数学.files/image547.gif) 在直线
在直线理科数学.files/image198.gif) 上,则
上,则理科数学.files/image550.gif) .
.
(2)理科数学.files/image552.gif) .
.
设理科数学.files/image554.gif) ,则
,则理科数学.files/image556.gif) ,点
,点理科数学.files/image200.gif) 到直线
到直线理科数学.files/image098.gif) 的距离
的距离理科数学.files/image560.gif)
理科数学.files/image562.gif) .
.
理科数学.files/image564.gif) ,由于直线
,由于直线理科数学.files/image198.gif) 与线段
与线段理科数学.files/image098.gif) 相交于
相交于理科数学.files/image096.gif) ,则
,则理科数学.files/image569.gif) ,则
,则理科数学.files/image571.gif) .
.
记理科数学.files/image573.gif) ,则
,则理科数学.files/image575.gif) .
.
其次,理科数学.files/image577.gif) ,同理求得
,同理求得理科数学.files/image202.gif) 到
到理科数学.files/image098.gif) 的中离:
的中离:理科数学.files/image581.gif) ,
,
设理科数学.files/image583.gif) ,即
,即理科数学.files/image585.gif) ,由
,由理科数学.files/image587.gif) 得
得理科数学.files/image589.gif) .
.
理科数学.files/image591.gif) ,
,
即理科数学.files/image593.gif) 且
且理科数学.files/image595.gif) 时,
时,理科数学.files/image597.gif) .
.
又理科数学.files/image599.gif) ,当
,当理科数学.files/image601.gif) 即
即理科数学.files/image603.gif) 时,
时,理科数学.files/image605.gif) .注意到
.注意到理科数学.files/image607.gif) ,由对称性,
,由对称性,理科数学.files/image609.gif) 时仍有
时仍有理科数学.files/image611.gif)
理科数学.files/image612.jpg) 故
故理科数学.files/image614.gif) ,进而
,进而理科数学.files/image616.gif) .
.
故四边形理科数学.files/image094.gif) 的面积:
的面积:
理科数学.files/image619.gif)
理科数学.files/image621.gif) ,
,
当理科数学.files/image603.gif) 时,
时,理科数学.files/image624.gif) .
.
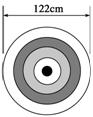 ⑴从4名男生和2名女生中任选3人参加演讲比赛。求所选3人中至少有1名女生概率。 ⑵射箭比赛的箭靶涂有5个彩色的分环,从外向内白色、黑色、蓝色、红色,靶心为金色,金色靶心叫“黄心”,奥运会的比赛靶面直径是122 cm,靶心直径12.2 cm,运动员在70米外射箭,假设都能中靶,且射中靶面内任一点是等可能的,求射中“黄心”的概率
⑴从4名男生和2名女生中任选3人参加演讲比赛。求所选3人中至少有1名女生概率。 ⑵射箭比赛的箭靶涂有5个彩色的分环,从外向内白色、黑色、蓝色、红色,靶心为金色,金色靶心叫“黄心”,奥运会的比赛靶面直径是122 cm,靶心直径12.2 cm,运动员在70米外射箭,假设都能中靶,且射中靶面内任一点是等可能的,求射中“黄心”的概率
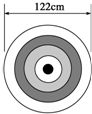 (1)从4名男生和2名女生中任选3人参加演讲比赛.求所选3人中至少有1名女生的概率.
(1)从4名男生和2名女生中任选3人参加演讲比赛.求所选3人中至少有1名女生的概率. (1)从4名男生和2名女生中任选3人参加演讲比赛.求所选3人中至少有1名女生的概率.
(1)从4名男生和2名女生中任选3人参加演讲比赛.求所选3人中至少有1名女生的概率.