摘要：∵0≤p≤1,∴当p=时,max=2.
网址：http://m.1010jiajiao.com/timu_id_14965[举报]
在平面直角坐标系xoy上，给定抛物线L：y=
x2．实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}．
（1）过点，A（p0，
p02）（p0≠0），作L的切线交y轴于点B．证明：对线段AB上的任一点Q（p，q），有φ（p，q）=
；
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
），E′（p2，
p22），l1，l2与y轴分别交于F，F′．线段EF上异于两端点的点集记为X．证明：M（a，b）∈X?|P1|＜|P2|?φ（a，b）=
．
（3）设D={ （x，y）|y≤x-1，y≥
（x+1）2-
}．当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）
查看习题详情和答案>>
| 1 |
| 4 |
（1）过点，A（p0，
| 1 |
| 4 |
| |p0| |
| 2 |
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
| 1 |
| 4 |
| p | 2 1 |
| 1 |
| 4 |
| |p1| |
| 2 |
（3）设D={ （x，y）|y≤x-1，y≥
| 1 |
| 4 |
| 5 |
| 4 |
在平面直角坐标系xoy上，给定抛物线L：y=
x2．实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}．
（1）过点，A（p0，
p02）（p0≠0），作L的切线交y轴于点B．证明：对线段AB上的任一点Q（p，q），有φ（p，q）=
；
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
），E′（p2，
p22），l1，l2与y轴分别交于F，F′．线段EF上异于两端点的点集记为X．证明：M（a，b）∈X?|P1|＜|P2|?φ（a，b）=
．
（3）设D={ （x，y）|y≤x-1，y≥
（x+1）2-
}．当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）
查看习题详情和答案>>
| 1 |
| 4 |
（1）过点，A（p0，
| 1 |
| 4 |
| |p0| |
| 2 |
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
| 1 |
| 4 |
| p | 21 |
| 1 |
| 4 |
| |p1| |
| 2 |
（3）设D={ （x，y）|y≤x-1，y≥
| 1 |
| 4 |
| 5 |
| 4 |
在平面直角坐标系xOy上，给定抛物线L：y=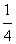
x2，实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}.
（1）过点A（p0，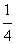
p0）（p0≠0）作L的切线教y轴于点B。证明：对线段AB上任一点Q（p，q）有φ（p，q）=
；
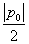（2）设M（a，b）是定点，其中a，b满足a2-4b>0，a≠0。过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，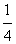
p12），E′（p2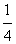，p22），l1，l2与y轴分别交与F，F'。线段EF上异于两端点的点集记为X。证明：M（a，b）∈X
|P1|＞|P2|φ（a，b）=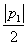
；
（3）设D={（x，y）|y≤x-1，y≥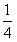
（x+1）2-
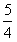}，当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）。
查看习题详情和答案>>
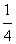x2，实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}.（1）过点A（p0，
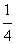p0）（p0≠0）作L的切线教y轴于点B。证明：对线段AB上任一点Q（p，q）有φ（p，q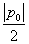）=；（2）设M（a，b）是定点，其中a，b满足a2-4b>0，a≠0。过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
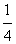p12），E′（p2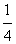，p22），l1，l2与y轴分别交与F，F'。线段EF上异于两端点的点集记为X。证明：M（a，b）∈X|P1|＞|P2|φ（a，b）=；（3）设D={（x，y）|y≤x-1，y≥
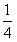（x+1）2-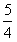}，当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）。在平面直角坐标系xoy上，给定抛物线L：y=
x2．实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}．
（1）过点，A（p0，p02）（p0≠0），作L的切线交y轴于点B．证明：对线段AB上的任一点Q（p，q），有φ（p，q）=
；
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，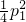
），E′（p2，p22），l1，l2与y轴分别交于F，F′．线段EF上异于两端点的点集记为X．证明：M（a，b）∈X?|P1|＜|P2|?φ（a，b）=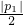
．
（3）设D={ （x，y）|y≤x-1，y≥（x+1）2-
}．当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）
查看习题详情和答案>>
在平面直角坐标系xoy上，给定抛物线L：y=
x2．实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}．
（1）过点，A（p，
p2）（p≠0），作L的切线交y轴于点B．证明：对线段AB上的任一点Q（p，q），有φ（p，q）=
；
（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
），E′（p2，
p22），l1，l2与y轴分别交于F，F′．线段EF上异于两端点的点集记为X．证明：M（a，b）∈X?|P1|＜|P2|?φ（a，b）=
．
（3）设D={ （x，y）|y≤x-1，y≥
（x+1）2-
}．当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）
查看习题详情和答案>>
x2．实数p，q满足p2-4q≥0，x1，x2是方程x2-px+q=0的两根，记φ（p，q）=max{|x1|，|x2|}．（1）过点，A（p，
p2）（p≠0），作L的切线交y轴于点B．证明：对线段AB上的任一点Q（p，q），有φ（p，q）=；（2）设M（a，b）是定点，其中a，b满足a2-4b＞0，a≠0．过M（a，b）作L的两条切线l1，l2，切点分别为E（p1，
），E′（p2，p22），l1，l2与y轴分别交于F，F′．线段EF上异于两端点的点集记为X．证明：M（a，b）∈X?|P1|＜|P2|?φ（a，b）=．（3）设D={ （x，y）|y≤x-1，y≥
（x+1）2-}．当点（p，q）取遍D时，求φ（p，q）的最小值 （记为φmin）和最大值（记为φmax）查看习题详情和答案>>