摘要:∵= ∴CQ=DQ×=在Rt△APC中.PC=BQ=BD+DQ=15.∠ACP=30°AP=PCtan30°=15×=.∴AB=AP+PB=∵BG=14-3=11.∴AB?BG ∴不需要封闭人行道.
网址:http://m.1010jiajiao.com/timu_id_14602[举报]
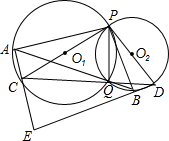 如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的直径PC=4,⊙O2的直径PD=2
如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的直径PC=4,⊙O2的直径PD=2| 2 |
(1)求证:C、Q、D三点在一直线上;
(2)求证:
| PA |
| PB |
| 2 |
(3)若PQ=2,试求∠E度数.
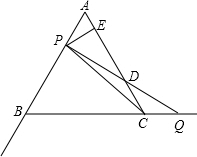 △ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.(1)如图,当点P在边AB(与点A、B不重合)上,问:
①线段PD与线段DQ之间有怎样的大小关系?试证明你的结论.
②随着点P、Q的移动,线段DE的长能否确定?若能,求出DE的长;若不能,简要说明理由;
(2)当点P在射线AB上,若设AP=x,CD=y,求:
①y与x之间的函数关系式,并写出x的取值范围;
②当x为何值时,△PCQ的面积与△ABC的面积相等. 查看习题详情和答案>>
如图1,在长为44,宽为12的矩形PQRS中,将一张直角三角形纸片ABC和一张正方形纸片DEFG如图放置,其中边AB、DE在PQ上,边EF在QR上,边BC、DG在同一直线上,且Rt△ABC两直角边BC=6,AB=8,正方形DEFG的边长为4.从初始时刻开始,三角形纸片ABC,沿AP方向以每秒1个单位长度的速度向左平移;同时正方形纸片DEFG,沿QR方向以每秒2个单位长度的速度向上平移,当边GF落在SR上时,纸片DEFG立即沿RS方向以原速度向左平移,直至G点与S点重合时,两张纸片同时停止移动.设平移时间为x秒.
(1)请填空:当x=2时,CD=
(2)如图2,当纸片DEFG沿QR方向平移时,连接CD、DQ和CQ,求平移过程中△CDQ的面积S与x的函数关系式,并写出自变量x的取值范围(这里规定线段的面积为零);
(3)如图3,当纸片DEFG沿RS方向平移时,是否存在这样的时刻x,使以A、C、D为顶点的三角形是等腰三角形?若存在,求出对应x的值;若不存在,请说明理由.



查看习题详情和答案>>
(1)请填空:当x=2时,CD=
2
| 2 |
2
,DQ=| 2 |
4
| 2 |
4
,此时CD+DQ| 2 |
=
=
CQ(请填“<”、“=”、“>”);(2)如图2,当纸片DEFG沿QR方向平移时,连接CD、DQ和CQ,求平移过程中△CDQ的面积S与x的函数关系式,并写出自变量x的取值范围(这里规定线段的面积为零);
(3)如图3,当纸片DEFG沿RS方向平移时,是否存在这样的时刻x,使以A、C、D为顶点的三角形是等腰三角形?若存在,求出对应x的值;若不存在,请说明理由.



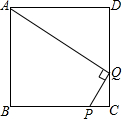 如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=
如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=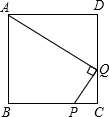 如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,PQ⊥AQ,则BP=
如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,PQ⊥AQ,则BP=