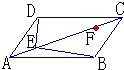28、如图，在?ABCD中，点E、F在对角线AC上，且AE=CF．
（1）请你以点F和图中以表明字母的另一点为端点作一条线段．
你连接的线段是：；
（2）猜想并说明这条线段和图中的某一条已有线段相等．
猜想：．
理由：

（2009•保定二模）正方形ABCD中，点P是CD所在直线上一点，连接PA，分别过B、D作BE⊥PA、DF⊥PA，垂足分别为E、F．
（1）如图1，当点P在DC边上时，通过观察或测量，猜想线段BE、DF、EF应满足怎样的数量关系，并证明你的猜想；
（2）如图2，当点P在DC的延长线上时，通过观察或测量，猜想线段BE、DF、EF应满足怎样的数量关系，并证明你的猜想；
（3）如图3，当点P在CD的延长线上时，线段BE、DF、EF又具有怎样的数量关系，请直接写出结论（不必进行证明）．

如图，△ABC中，∠BAC=90゜，AC=2AB，D为AC的中点，E为△ABC外一点，且EA=ED，EA⊥ED，试猜想线段BE和CE的数量关系和位置关系，并证明．

（2013•大兴区二模）已知：如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，以AD为斜边在△ABC外作等腰直角三角形AED，连结BE、EC．试猜想线段BE和EC的数量关系及位置关系，并证明你的猜想．