网址:http://m.1010jiajiao.com/timu_id_140152[举报]
如图, ,
,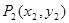 ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,…
均为斜边在
,…
均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

【解析】第一问利用有 ,
, 得到
得到
第二问证明:①当 时,可求得
时,可求得 ,命题成立;②假设当
,命题成立;②假设当 时,命题成立,即有
时,命题成立,即有 则当
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得
第三问

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即

解:(1)依题意,有 ,
, ,………………4分
,………………4分
(2)证明:①当 时,可求得
时,可求得 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当 时,命题成立,即有
时,命题成立,即有 ,……………………1分
,……………………1分
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得 .
.
即
解得 (
( 不合题意,舍去)
不合题意,舍去)
即当 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即
 .……………2分
.……………2分
由题意,有
 .
所以,
.
所以,
查看习题详情和答案>>
一自来水厂用蓄水池通过管道向所管辖区域供水.某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水 千吨.
千吨.
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
【解析】第一问中(1)设 小时后,蓄水池有水
小时后,蓄水池有水 千吨.依题意,
千吨.依题意, 当
当 ,即
,即 (小时)时,蓄水池的水量最少,只有1千吨
(小时)时,蓄水池的水量最少,只有1千吨
第二问依题意, 解得:
解得:
解:(1)设 小时后,蓄水池有水
小时后,蓄水池有水 千吨.………………………………………1分
千吨.………………………………………1分
依题意, …………………………………………4分
…………………………………………4分
当 ,即
,即 (小时)时,蓄水池的水量最少,只有1千吨. ………2分
(小时)时,蓄水池的水量最少,只有1千吨. ………2分
(2)依题意, ………………………………………………3分
………………………………………………3分
解得: . …………………………………………………………………3分
. …………………………………………………………………3分
所以,当天有8小时会出现供水紧张的情况
查看习题详情和答案>>
(1)依题意分别计算该学生选修书法、绘画、雕塑三门校本选修课的概率;
(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,求随机变量ξ的分布列和数学期望.