摘要： 解(1)连接B1C.交BC1于点O.则O为B1C的中点. ∵D为AC中点 ∴OD∥B1A 又B1A平面BDC1.OD平面BDC1 ∴B1A∥平面BDC1 -----6分 (2)∵AA1⊥面ABC.BC⊥AC.AA1∥CC1 ∴CC1⊥面ABC 则BC⊥平面AC1.CC1⊥AC 如图以C为坐标原点.CA所在直线为X轴.CB所在直线为Y轴.所在直线为轴建立空间直角坐标系 则C1 D ∴ 设平面的法向量为 则 又平面BDC的法向量为 ∴二面角C1―BD―C的余弦值:cos -----12分
网址：http://m.1010jiajiao.com/timu_id_140151[举报]
（2009•嘉定区二模）图1所示的是一个长方体截去一个角所得多面体的直观图．图2是它的主视图和左视图（单位：cm）．
（1）在主视图下面按照三视图的要求画出该多面体的俯视图；
（2）按照图2给出的尺寸，求该多面体的体积；
（3）在图1中连接B1C，求异面直线EF和B1C所成角的大小（结果用反三角函数表示）．
查看习题详情和答案>>
（1）在主视图下面按照三视图的要求画出该多面体的俯视图；
（2）按照图2给出的尺寸，求该多面体的体积；
（3）在图1中连接B1C，求异面直线EF和B1C所成角的大小（结果用反三角函数表示）．
图1所示的是一个长方体截去一个角所得多面体的直观图．图2是它的主视图和左视图（单位：cm）．
（1）在主视图下面按照三视图的要求画出该多面体的俯视图；
（2）按照图2给出的尺寸，求该多面体的体积；
（3）在图1中连接B1C，求异面直线EF和B1C所成角的大小（结果用反三角函数表示）．
查看习题详情和答案>>
图1所示的是一个长方体截去一个角所得多面体的直观图．图2是它的主视图和左视图（单位：cm）．
（1）在主视图下面按照三视图的要求画出该多面体的俯视图；
（2）按照图2给出的尺寸，求该多面体的体积；
（3）在图1中连接B1C，求异面直线EF和B1C所成角的大小（结果用反三角函数表示）．
查看习题详情和答案>>
（1）在主视图下面按照三视图的要求画出该多面体的俯视图；
（2）按照图2给出的尺寸，求该多面体的体积；
（3）在图1中连接B1C，求异面直线EF和B1C所成角的大小（结果用反三角函数表示）．
查看习题详情和答案>>
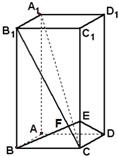如图，己知正四棱棱柱AC1中，AB=BC=1，BB1=2，连接B1C和A1C