摘要： 解解:(Ⅰ)性别 成绩合格不合格合计男性451055女性302050合计7530105--------------- (Ⅱ)随机抽查这批学员中的任意一个学员.有105种不同的抽查方法.由于是女学员且考试不及格的由20人.所以有20种不同的抽法.因此由古典概型的计算公式得抽到女学员且考试不合格的概率是. --------------- (Ⅲ)假设性别与考试是否合格无关..所以有的把握认为性别与考试是否合格有关.---12分
网址：http://m.1010jiajiao.com/timu_id_140142[举报]
（2013•东莞二模）通过随机询问某景区110名游客对景区的服务是否满意，得到如下的列联表：
性别与对景区的服务是否满意 单位：名
（I）从这50名女游客中按对景区的服务是否满意采取分层抽样，抽取一个容量为5的样本，闷样本中浦意与不满意的女游客各有多少名？
（II）从（I）中的5名女游客样本中随机选取两名作深度访谈，求选到满意与不满意的女游客各一名的概率；
（III》很招以上列联表，问有多大把握认为“游客性别与对景区的服务满意”有关．
查看习题详情和答案>>
性别与对景区的服务是否满意 单位：名
| 男 | 女 | 总计 | |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
（II）从（I）中的5名女游客样本中随机选取两名作深度访谈，求选到满意与不满意的女游客各一名的概率；
（III》很招以上列联表，问有多大把握认为“游客性别与对景区的服务满意”有关．
为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行出样检查，测得身高情况的统计图如下：
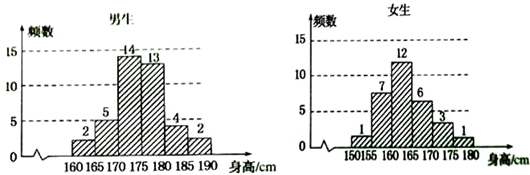
（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在170～185cm之间的概率；
（Ⅲ）从样本中身高在180～190cm之间的男生中任选2人，求至少有1人身高在185～190cm之间的概率． 查看习题详情和答案>>
（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在170～185cm之间的概率；
（Ⅲ）从样本中身高在180～190cm之间的男生中任选2人，求至少有1人身高在185～190cm之间的概率． 查看习题详情和答案>>
某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：
为了检验主修统计专业是否与性别有关系，根据表中的数据，得到k=
≈4.84．因为K2≥3.841，所以断定主修统计专业与性别有关系，这种判断出错的可能性为
查看习题详情和答案>>
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| 50(13×20-10×7)2 |
| 23×27×20×30 |
0.05
0.05
．
（2012•辽宁）电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．（Ⅰ）根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？
| 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P（ K2≥k） | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
随着田径110米栏运动员刘翔的崛起，大家对这项运动的关注度也大大提高，有越来越多的人参与到了这项运动中，为了解某班学生对了解110米栏运动是否与性别有关，对本班同学进行了问卷调查，得到了如下的列联表：
（1）用分层抽样的方法在不了解110米栏运动的学生中抽5人，其中男、女生各抽取多少人？
（2）在上述抽取的5人中选2人，求至少有一人是男生的概率；
（3）你有95%还是99%的把握认为是否了解110米栏与性别有关？并证明你的结论．
附：k2=
，
查看习题详情和答案>>
| 了解110米栏 | 了解110米栏 | 合计 | |
| 男生 | 22 | 8 | 30 |
| 女生 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
（2）在上述抽取的5人中选2人，求至少有一人是男生的概率；
（3）你有95%还是99%的把握认为是否了解110米栏与性别有关？并证明你的结论．
附：k2=
| n(n11n12-n12n21)2 |
| n1+n2+n+1n+2 |
| P（k2≥k） | 0.05 | 0.01 |
| k | 3.841 | 6.635 |