摘要：∵CG平面FGC ∴平面ABD⊥平面FGC在平面ABD内作EH⊥FG.垂足为H ∴EH⊥平面FGC作HK⊥FC.垂足为K.连结EK.故EK⊥FC∴∠EKH为二面角E―FC―G的平面角 --10分
网址：http://m.1010jiajiao.com/timu_id_13612[举报]
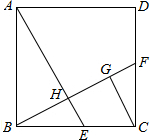如图，在正方形ABCD中，E、F分别是边BC、CD的中点，AE交BF于点H，CG∥AE交BF于点G．下列结论：①tan∠HBE=cot∠HEB；②CG•BF=BC•CF；③BH=FG；④| BC2 |
| CF2 |
| BG |
| GF |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
如图，在正方形ABCD中，E、F分别是边BC、CD的中点，AE交BF于点H，CG∥AE交BF于点G．下列结论：①tan∠HBE=cot∠HEB；②CG•BF=BC•CF；③BH=FG；④
| BC2 |
| CF2 |
| BG |
| GF |
其中正确的序号是
①②④
①②④
．
如图，已知在Rt△ABC中，∠ACB=90°，AC=6，BC=8，BE平分∠ABC交AC于点E，EF⊥AB，垂足为F．（1）求EF的长度；
（2）作CD⊥AB，垂足为D，CD与BE相交于G，试说明：CE=CG；
（3）连接FG，试说明：四边形CEFG是菱形．
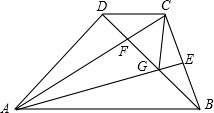如图，在梯形ABCD中，DC∥AB，AB=AC，E为BC的中点，BD交AC于F，交AE于G，连接CG．下列结论中：
．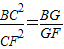