摘要:[解答](Ⅰ)f(x)的定义域为----------------
网址:http://m.1010jiajiao.com/timu_id_135395[举报]
已知函数f(x)=x2-ax+b
(Ⅰ)【理科】若b=4时,f(x)≥0对x∈(0,4)恒成立,求a的范围;
【文科】若b=4时,f(x)≥0对x∈R恒成立,求a的范围;
(Ⅱ)若f(-1)≥0,f(0)≤0,f(2)≥0,求f(3)的范围.
查看习题详情和答案>>
(Ⅰ)【理科】若b=4时,f(x)≥0对x∈(0,4)恒成立,求a的范围;
【文科】若b=4时,f(x)≥0对x∈R恒成立,求a的范围;
(Ⅱ)若f(-1)≥0,f(0)≤0,f(2)≥0,求f(3)的范围.
已知函数f(x)(x∈R)满足f(x)=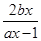 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1=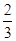 ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)=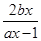 ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即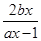 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)=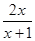 .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
=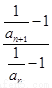 =
=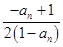 =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1=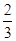 ,∴b1=
,∴b1=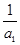 -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an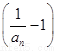 =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn=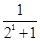 +
+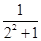 +…+
+…+ <
<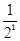 +
+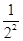 +…+
+…+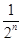
=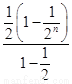 =1-
=1-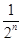 <1(n∈N*).
<1(n∈N*).
查看习题详情和答案>>