网址:http://m.1010jiajiao.com/timu_id_130255[举报]
1. 由函数 知,当
知,当 时,
时, ,且
,且 ,则它的反函数过点(3,4),故选A.
,则它的反函数过点(3,4),故选A.
2.∵ ,∴
,∴ ,则
,则 ,即
,即 ,
, .
. ,选B.
,选B.
3. 由平行四边形法则, ,
,
∴ ,
,
又 ,
,
∴ ,当P为
,当P为 中点时,取得最小值
中点时,取得最小值 .选B.
.选B.
4. 设 是椭圆的一个焦点,它是椭圆三个顶点
是椭圆的一个焦点,它是椭圆三个顶点 ,
, ,
, 构成的三角形的垂心(如图).由
构成的三角形的垂心(如图).由 有
有 ,即
,即 ,∴
,∴ ,得
,得 ,解得
,解得 ,选A.
,选A.
5. 设正方形边长为 ,
, ,则
,则 ,
, .在
.在 由正弦定理得
由正弦定理得
 ,又在
,又在 由余弦定理得
由余弦定理得 ,于是
,于是 ,
, ,选C.
,选C.
 6.
6.  在底面
在底面 上的射影
上的射影 知,
知, 为斜线
为斜线 在平面
在平面 上的射影,∵
上的射影,∵ ,由三垂线定理得
,由三垂线定理得 ,∵
,∵ ,所以直线
,所以直线 与直线
与直线 重合,选A.
重合,选A.
7. 过A作抛物线 的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线
的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线 交右准线于
交右准线于 则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长
则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长 =|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
=|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
由可得两曲线的交点x=,xB∈(,2),
∴3+xB∈(,4),即△ANB周长 取值范围是(,4),选B.
取值范围是(,4),选B.
8. 先将3,5两个奇数排好,有 种排法,再将4,6两个偶数插入3,5中,有
种排法,再将4,6两个偶数插入3,5中,有 种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为
种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为 ,选B.
,选B.
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴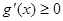 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
查看习题详情和答案>>
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1, f(x1)),B(x2, f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
当 时
时 单调递减;当
单调递减;当 时
时 单调递增,故当
单调递增,故当 时,
时, 取最小值
取最小值
于是对一切 恒成立,当且仅当
恒成立,当且仅当 . ①
. ①
令 则
则
当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减.
单调递减.
故当 时,
时, 取最大值
取最大值 .因此,当且仅当
.因此,当且仅当 时,①式成立.
时,①式成立.
综上所述, 的取值集合为
的取值集合为 .
.
(Ⅱ)由题意知, 令
令 则
则


令 ,则
,则 .当
.当 时,
时, 单调递减;当
单调递减;当 时,
时, 单调递增.故当
单调递增.故当 ,
, 即
即
从而 ,
, 又
又

所以
 因为函数
因为函数 在区间
在区间 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在 使
使 即
即 成立.
成立.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出 取最小值
取最小值 对一切x∈R,f(x)
对一切x∈R,f(x)  1恒成立转化为
1恒成立转化为 从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
查看习题详情和答案>>
已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
查看习题详情和答案>>
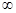 )上的函数
)上的函数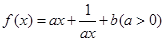
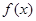 的最小值;
的最小值;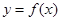 在点
在点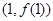 处的切线方程为
处的切线方程为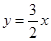 ,求
,求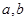 的值。
的值。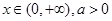 ,故
,故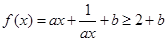 ,取等号的条件是
,取等号的条件是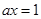 ,即
,即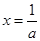 。
。 ,由
,由 ,求得
,求得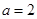 ,又由
,又由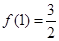 ,可得
,可得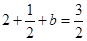 ,解得
,解得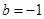

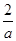 )
)

