网址:http://m.1010jiajiao.com/timu_id_130205[举报]
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.

【解析】(Ⅰ)因为
又 是平面PAC内的两条相较直线,所以BD
是平面PAC内的两条相较直线,所以BD 平面PAC,
平面PAC,
而 平面PAC,所以
平面PAC,所以 .
.
(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD 平面PAC,
平面PAC,
所以 是直线PD和平面PAC所成的角,从而
是直线PD和平面PAC所成的角,从而
 .
.
由BD 平面PAC,
平面PAC, 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由
 ,得PD=2OD.因为四边形ABCD为等腰梯形,
,得PD=2OD.因为四边形ABCD为等腰梯形, ,所以
,所以 均为等腰直角三角形,从而梯形ABCD的高为
均为等腰直角三角形,从而梯形ABCD的高为 于是梯形ABCD面积
于是梯形ABCD面积
 在等腰三角形AOD中,
在等腰三角形AOD中,
所以
故四棱锥 的体积为
的体积为 .
.

【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD 平面PAC即可,第二问由(Ⅰ)知,BD
平面PAC即可,第二问由(Ⅰ)知,BD 平面PAC,所以
平面PAC,所以 是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由
是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由 算得体积
算得体积
查看习题详情和答案>>
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1, f(x1)),B(x2, f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
当 时
时 单调递减;当
单调递减;当 时
时 单调递增,故当
单调递增,故当 时,
时, 取最小值
取最小值
于是对一切 恒成立,当且仅当
恒成立,当且仅当 . ①
. ①
令 则
则
当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减.
单调递减.
故当 时,
时, 取最大值
取最大值 .因此,当且仅当
.因此,当且仅当 时,①式成立.
时,①式成立.
综上所述, 的取值集合为
的取值集合为 .
.
(Ⅱ)由题意知, 令
令 则
则


令 ,则
,则 .当
.当 时,
时, 单调递减;当
单调递减;当 时,
时, 单调递增.故当
单调递增.故当 ,
, 即
即
从而 ,
, 又
又

所以
 因为函数
因为函数 在区间
在区间 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在 使
使 即
即 成立.
成立.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出 取最小值
取最小值 对一切x∈R,f(x)
对一切x∈R,f(x)  1恒成立转化为
1恒成立转化为 从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
查看习题详情和答案>>
在△ABC中, 为三个内角
为三个内角 为三条边,
为三条边, 且
且
(I)判断△ABC的形状;
(II)若 ,求
,求 的取值范围.
的取值范围.
【解析】本题主要考查正余弦定理及向量运算
第一问利用正弦定理可知,边化为角得到

所以得到B=2C,然后利用内角和定理得到三角形的形状。
第二问中,

得到。
(1)解:由 及正弦定理有:
及正弦定理有:
∴B=2C,或B+2C ,若B=2C,且
,若B=2C,且 ,∴
,∴ ,
, ;∴B+2C
;∴B+2C ,则A=C,∴
,则A=C,∴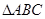 是等腰三角形。
是等腰三角形。
(2)

查看习题详情和答案>>
△ABC中,内角A、B、C成等差数列,其对边a、b、c满足 ,求A。
,求A。
【解析】本试题主要考查了解三角形的运用,
因为

【点评】该试题从整体来看保持了往年的解题风格,依然是通过边角的转换,结合了三角形的内角和定理的知识,以及正弦定理和余弦定理,求解三角形中的角的问题。试题整体上比较稳定,思路也比较容易想,先将利用等差数列得到角B,然后利用余弦定理求解运算得到A。
查看习题详情和答案>>
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
查看习题详情和答案>>