网址:http://m.1010jiajiao.com/timu_id_127612[举报]
一.选择题:



 二、填空题: 13.
二、填空题: 13.  14.
14.  15.
15.  16.
16. 
三.解答题
17.解:⑴f(x)= sinxcosx+ +
+ cos2x =
sin(2x+
cos2x =
sin(2x+ )+
)+
T=π,2 kπ- ≤2x+
≤2x+ ≤2 kπ+
≤2 kπ+ ,k∈Z,
,k∈Z,
最小正周期为π,单调增区间[kπ- ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
⑵由sin(2A+ )=0,
)=0, <2A+
<2A+ <
< ,
,
∴2A+ =π或2π,∴A=
=π或2π,∴A= 或
或
18. 解:(1)
(2)设各等奖的奖金数为ξ则
ξ
5000
1000
20
0
P
0.001
0.009
0.09
0.9
∴Eξ=5+9+1.8+0=15.8(元)
19.解:(1) 平面
平面
∵二面角 为直二面角,且
为直二面角,且 ,
,
 平面
平面
 平面
平面 .
.
(2)连接 与高
与高 交于
交于 ,连接
,连接 是边长为2的正方形,
是边长为2的正方形,  ,
,
 二平面
二平面 ,由三垂线定理逆定理得
,由三垂线定理逆定理得
 是二面角
是二面角 的平面角
的平面角
由(1) 平面
平面 ,
,
 .
.
在 中,
中,
∴在 中,
中,
故二面角 等于
等于 .
.
(2)可用向量法
20. 解:(1)因
故 是公比为
是公比为 的等比数列,且
的等比数列,且
故 .
.
(2)由 得
得



注意到 ,可得
,可得 ,即
,即
记数列 的前
的前 项和为
项和为 ,则
,则
 两式相减得:
两式相减得:

故
从而
 .
.
21.解:(1)由 得
得
∴椭圆 的方程为:
的方程为: .
.
(2)设直线 的方程为:
的方程为:
由 得
得


由此得 . ①
. ①
设 与椭圆
与椭圆 的交点为
的交点为 ,则
,则
由 得
得
 ,整理得
,整理得
 ,整理得
,整理得
 时,上式不成立,
时,上式不成立, ②
②
由式①、②得
 或
或
∴ 取值范围是
取值范围是 .
.
22.,解(1)
 故
故 在
在 递减
递减
(2) 记
记

再令 
 在
在 上递增
上递增
 ,从而
,从而  故
故 在
在 上也单调递增
上也单调递增

设等比数列{an}的前n项和为Sn,已知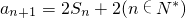 .
.
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
查看习题详情和答案>>
(1)求数列{an}的公比q和首项a1的值;
(2)若常数P使得对一切正整数n都有an+1=PSn+1成立,求P的值;
(3)(理)求![]() .
.
 .
.(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
查看习题详情和答案>>
 .
.(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
查看习题详情和答案>>