网址:http://m.1010jiajiao.com/timu_id_127340[举报]
一、
1.C 2.D 3.B 4.D 5.D 6.B 7.D 8.A 9.A 10.C
11.D 12.A
1~11.略
12.解:,
在是减函数,由,得,,故选A.
二、
13.0.8 14. 15. 16.①③
三、
17.解:(1)
的单调递增区间为
(2)
18.解:(1)当时,有种坐法,
,即,
或舍去.
(2)的可能取值是0,2,3,4
又
的概率分布列为
0
2
3
4
则.
19.解:(1)时,,
又 ,
是一个以2为首项,8为公比的等比数列
(2)
最小正整数.
20.解法一:
(1)设交于点
平面.
作于点,连接,则由三垂线定理知:是二面角的平面角.
由已知得,
,
∴二面角的大小的60°.
(2)当是中点时,有平面.
证明:取的中点,连接、,则,
,故平面即平面.
又平面,
平面.
解法二:由已知条件,以为原点,以、、为轴、轴、轴建立空间直角坐标系,则
(1),
,设平面的一个法向量为,
则取
设平面的一个法向量为,则取.
二面角的大小为60°.
(2)令,则,
,
由已知,,要使平面,只需,即
则有,得当是中点时,有平面.
21.解:(1)由条件得,所以椭圆方程是.
(2)易知直线斜率存在,令
由
由,
即得
,
即
得
将代入
有
22.解:(1)
在上为减函数,时,恒成立,
即恒成立,设,则
时,在(0,)上递减速,
.
(2)若即有极大值又有极小值,则首先必需有两个不同正要,,
即有两个不同正根
令
∴当时,有两个不同正根
不妨设,由知,
时,时,时,
∴当时,既有极大值又有极小值.
(本小题满分10分)
已知椭圆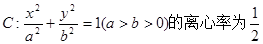 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线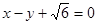 相切。
相切。
(1)求椭圆C的方程;
(2)设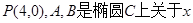 轴对称的任意两个不同的点,连结PB交椭圆C于另一点E,证明:直线AE与x轴相交于定点Q;
轴对称的任意两个不同的点,连结PB交椭圆C于另一点E,证明:直线AE与x轴相交于定点Q;
(3)在(2)的条件下,过点Q的直线与椭圆C交于M、N两点,求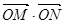 的取值范围。
的取值范围。
查看习题详情和答案>>
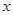 轴上,离心率为
轴上,离心率为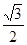 ,且经过点
,且经过点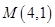 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B. 的取值范围。
的取值范围。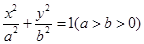 的离心率
的离心率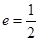 ,且原点
,且原点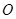 到直线
到直线 的距离为
的距离为 .
.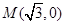 作直线与椭圆C交于
作直线与椭圆C交于 两点,求
两点,求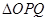 面积的最大值.
面积的最大值. 的离心率
的离心率 ,且原点
,且原点 到直线
到直线 的距离为
的距离为 .
. 作直线与椭圆C交于
作直线与椭圆C交于 两点,求
两点,求 面积的最大值.
面积的最大值.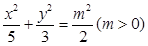 ,经过椭圆
,经过椭圆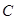 的右焦点F且斜率为
的右焦点F且斜率为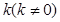 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在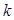 ,使对任意
,使对任意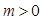 ,总有
,总有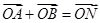 成立?若存在,求出所有
成立?若存在,求出所有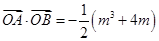 ,求实数
,求实数