摘要:由正弦定理得.即.
网址:http://m.1010jiajiao.com/timu_id_126917[举报]
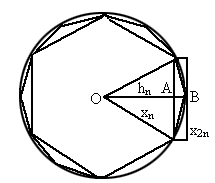
如图,设圆的半径为1,弦心距为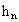 ;正n边形的边长为
;正n边形的边长为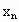 ,面积为
,面积为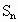 .由勾股定理,得
.由勾股定理,得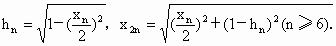
容易知道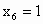 .
.
观察图1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即
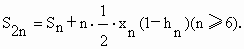
利用这个递推公式,我们可以得到:
正六边形的面积
正十二边形的面积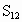 ________;
________;
正二十四边形的面积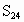 ________;
________;
…
请问n的输入值满足什么条件?n的输出组表示什么?当n不断增大, 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
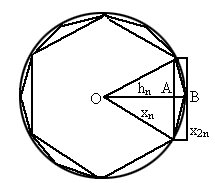
如图,设圆的半径为
1,弦心距为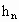 ;正n边形的边长为
;正n边形的边长为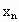 ,面积为
,面积为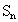 .由勾股定理,得
.由勾股定理,得
容易知道
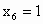 .
.
观察图
1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即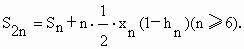
利用这个递推公式,我们可以得到:
正六边形的面积
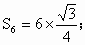
正十二边形的面积
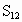 ________;
________;
正二十四边形的面积
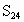 ________;
________;
…
请问
n的输入值满足什么条件?n的输出组表示什么?当n不断增大,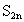 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
已知 中,内角
中,内角 的对边的边长分别为
的对边的边长分别为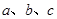 ,且
,且
(I)求角 的大小;
的大小;
(II)若 求
求 的最小值.
的最小值.
【解析】第一问,由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
第二问,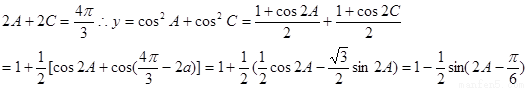
三角函数的性质运用。
解:(Ⅰ)由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
(Ⅱ)由(Ⅰ)可知
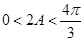 ,
, ,则当
,则当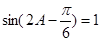 ,即
,即 时,y的最小值为
时,y的最小值为 .
.
查看习题详情和答案>>
 .]
.] 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, ,
, ,求
,求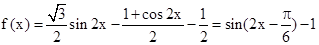

 ,由正弦定理,得
,由正弦定理,得 ,①
,①  ,即
,即 ,②
,②