摘要：14．数列满足,其中为常数．若存在实数,使得数列为等差数列或等比数列,则数列的通项公式 ．
网址：http://m.1010jiajiao.com/timu_id_126892[举报]
满足
,其中
为常数．若存在实数
．若存在实常数k和b，使得函数F（x）和G（x）对其公共定义域上的任意实数x都满足：F（x）≥kx+b和G（x）≤kx+b恒成立，则称此直线y=kx+b为F（x）和G（x）的“隔离直线”．已知函数h（x）=x2，m（x）=2elnx（e为自然对数的底数），φ（x）=x-2，d（x）=-1．
有下列命题：
①f（x）=h（x）-m（x）在x∈(0，
)递减；
②h（x）和d（x）存在唯一的“隔离直线”；
③h（x）和φ（x）存在“隔离直线”y=kx+b，且b的最大值为-
；
④函数h（x）和m（x）存在唯一的隔离直线y=2
x-e．
其中真命题的个数（ ）
有下列命题：
①f（x）=h（x）-m（x）在x∈(0，
| e |
②h（x）和d（x）存在唯一的“隔离直线”；
③h（x）和φ（x）存在“隔离直线”y=kx+b，且b的最大值为-
| 1 |
| 4 |
④函数h（x）和m（x）存在唯一的隔离直线y=2
| e |
其中真命题的个数（ ）
查看习题详情和答案>>
若存在实常数
和
，使得函数
和
对其公共定义域上的任意实数
都满足：
和
恒成立，则称此直线
为和的“隔离直线”．已知函数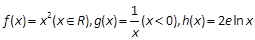
．有下列命题：
①
在
内单调递增;
②
和
之间存在“隔离直线”, 且b的最小值为-4;
③和之间存在“隔离直线”, 且k的取值范围是
;
④和
之间存在唯一的“隔离直线”
．
其中真命题的个数有( )．
| A．1个 | B．2个 | C．3个 | D．4个 |
递减；
；
．
和
，使得函数
和
对其公共定义域上的任意实数
都满足：
和
恒成立，则称此直线
为
．有下列命题：
在
内单调递增;
和
之间存在“隔离直线”, 且b的最小值为-4;
;
之间存在唯一的“隔离直线”
．