摘要：解:(1)依题意设双曲线C的方程为:.点P代入得．
网址：http://m.1010jiajiao.com/timu_id_12661[举报]
设椭圆
的左、右顶点分别为
，点
在椭圆上且异于两点，
为坐标原点.
（Ⅰ）若直线
与
的斜率之积为
，求椭圆的离心率；
（Ⅱ）若
，证明直线
的斜率
满足
【解析】(1)解：设点P的坐标为
.由题意，有
①
由
，得
，
由
，可得
，代入①并整理得
由于
，故
.于是
，所以椭圆的离心率
（2）证明：（方法一）
依题意，直线OP的方程为
，设点P的坐标为.
由条件得
消去
并整理得
②
由
，
及
，
得
.
整理得
.而
，于是
，代入②，
整理得
由
，故
，因此
.
所以
.
(方法二)
依题意，直线OP的方程为，设点P的坐标为.
由P在椭圆上，有
因为，
，所以
，即
③
由，，得整理得.
于是，代入③，
整理得
解得，
所以.
查看习题详情和答案>>
已知平面直角坐标系中的点A（-1，0），B（3，2），求直线AB的方程的一个算法如下，请将其补充完整。
第一步，根据题意设直线AB的方程为y=kx+b
第二步，将A（-1，0），B（3，2）代入第一步所设的方程，得到-k+b=0①；3k+b=2②，
第三步，（ ）
第四步，把第三步所得结果代入第一步所设的方程，得到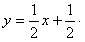
第五步，将第四步所得结果整理，得到方程x-2y+1=0。
查看习题详情和答案>>
第一步，根据题意设直线AB的方程为y=kx+b
第二步，将A（-1，0），B（3，2）代入第一步所设的方程，得到-k+b=0①；3k+b=2②，
第三步，（ ）
第四步，把第三步所得结果代入第一步所设的方程，得到
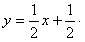
第五步，将第四步所得结果整理，得到方程x-2y+1=0。
（2013•重庆）设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2，使|A1B1|=|A2B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是（ ）
如图，设抛物线C的方程为y2=4x，O为坐标原点，P为抛物线的准线与其对称轴的交点，过焦点F且垂直于x轴的直线交抛物线于M、N两点，若直线PM与ON相交于点Q，则cos∠MQN=