摘要：即p=k=2时.数列{cn}的各项和为． -----------------12分当p<k时.3k?1=8.3k?p.因为k>p右边含有3的因数.而左边非3的倍数.所以不存在p.kÎN.
网址：http://m.1010jiajiao.com/timu_id_12644[举报]
（2008•宝山区二模）已知{an}是公差d大于零的等差数列，对某个确定的正整数k，有a12+ak+12≤M（M是常数）．
（1）若数列{an}的各项均为正整数，a1=2，当k=3时，M=100，写出所有这样数列的前4项；
（2）若数列{an}的各项均为整数，对给定的常数d，当数列由已知条件被唯一确定时，证明a1≤0；
（3）求S=ak+1+ak+2+…+a2k+1的最大值及此时数列{an}的通项公式．
查看习题详情和答案>>
（1）若数列{an}的各项均为正整数，a1=2，当k=3时，M=100，写出所有这样数列的前4项；
（2）若数列{an}的各项均为整数，对给定的常数d，当数列由已知条件被唯一确定时，证明a1≤0；
（3）求S=ak+1+ak+2+…+a2k+1的最大值及此时数列{an}的通项公式．
设无穷数列{an}的前n项和为Sn，且(3-p)Sn+2pan=3+p(n∈N*)，p为常数，p＜-3．
（1）求证：{an}是等比数列，写出{an}的通项公式；
（2）若数列{an}的公比q=f（p），无穷数列{bn}满足：b1=a1，bn=
f(bn-1)，(n≥2)，求证：{
}是等差数列，并写出{bn}的通项公式；
（3）设cn=
，在（2）的条件下，有
(bnlgan)=lg27，求数列{cn}的各项和．
查看习题详情和答案>>
（1）求证：{an}是等比数列，写出{an}的通项公式；
（2）若数列{an}的公比q=f（p），无穷数列{bn}满足：b1=a1，bn=
| 3 |
| 2 |
| 1 |
| bn |
（3）设cn=
| 1 |
| an-an+1 |
| lim |
| n→∞ |
设等比数列{an}的前n项和Sn，首项a1=1，公比q=f(λ)=
(λ≠-1，0)．
（Ⅰ）证明：Sn=（1+λ）-λan；
（Ⅱ）若数列{bn}满足b1=
，bn=f（bn-1）（n∈N*，n≥2），求数列{bn}的通项公式；
（Ⅲ）若λ=1，记cn=an(
-1)，数列{cn}的前项和为Tn，求证：当n≥2时，2≤Tn＜4．
查看习题详情和答案>>
| λ |
| 1+λ |
（Ⅰ）证明：Sn=（1+λ）-λan；
（Ⅱ）若数列{bn}满足b1=
| 1 |
| 2 |
（Ⅲ）若λ=1，记cn=an(
| 1 |
| bn |
．
，bn=f（bn-1）（n∈N*，n≥2），求数列{bn}的通项公式；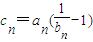
，数列{cn}的前项和为Tn，求证：当n≥2时，2≤Tn＜4．
．
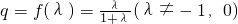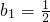，bn=f（bn-1）（n∈N*，n≥2），求数列{bn}的通项公式；
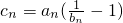，数列{cn}的前项和为Tn，求证：当n≥2时，2≤Tn＜4．