摘要:则有.所以()p=[1?()k]. ---------------11分当p≥k时3p?3p?k=8.即3p?k(3k?1)=8. 因为p.kÎN.所以只有p?k=0.k=2时.
网址:http://m.1010jiajiao.com/timu_id_12643[举报]
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
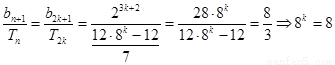
 ,
,
查看习题详情和答案>>
设P是△ABC内一点,△ABC三边上的高分别为hA、hB、hC,P到三边的距离依次为la、lb、lc,则有
+
+
=1;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是hA、hB、hC、hD,P到这四个面的距离依次是la、lb、lc、ld,则有
+
+
+
=1
+
+
+
=1.
查看习题详情和答案>>
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
 ,取函数f(x)=2-x-e-x,恒有fk(x)=f(x).则有( )
,取函数f(x)=2-x-e-x,恒有fk(x)=f(x).则有( )