摘要:[答案](1)证明从略 (2)四边形ABCD的面积的最小值为命题立意:本题主要考查直线与椭圆的位置关系.注意韦达定理以及基本不等式的运用.考查运用所学知识与方法解决问题的能力
网址:http://m.1010jiajiao.com/timu_id_125377[举报]
如图所示,四面体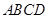 被一平面所截,截面
被一平面所截,截面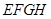 是一个平行四边形.求证:
是一个平行四边形.求证: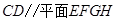 ;
;
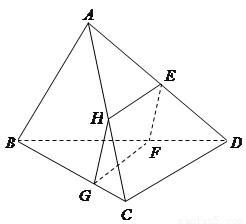
【答案】(理)证明: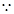 EH∥FG,EH
EH∥FG,EH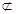 面
面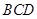 ,
,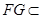 面
面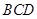
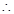 EH∥面
EH∥面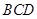 ,又
,又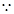 CD
CD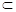 面
面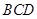 ,
,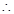 EH∥CD, 又EH
EH∥CD, 又EH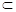 面EFGH,CD
面EFGH,CD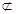 面EFGH
面EFGH
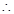 EH∥BD
EH∥BD
【解析】本试题主要是考查了空间四面体中线面位置关系的判定。
要证明线面平行可知通过线线平行,结合判定定理得到结论。
查看习题详情和答案>>
已知正方体ABCD-A1B1C1D1,
O是底面ABCD对角线的交点.
(1)求证:A1C⊥平面AB1D1;
(2)求 .
.

【解析】(1)证明线面垂直,需要证明直线垂直这个平面内的两条相交直线,本题只需证: 即可.
即可.
(2)可以利用向量法,也可以根据平面A1ACC1与平面AB1D1垂直,可知取B1D1的中点E,则 就是直线AC与平面AB1D1所成的角.然后解三角形即可.
就是直线AC与平面AB1D1所成的角.然后解三角形即可.
查看习题详情和答案>>
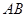 经过⊙
经过⊙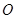 上的点
上的点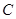 ,并且
,并且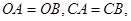 ⊙
⊙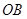 于
于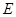 ,
,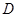 ,连接
,连接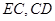 .
.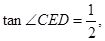 ⊙
⊙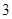 ,求
,求 的长.
的长.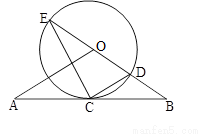
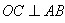 ;(II)根据
;(II)根据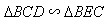 ,
,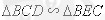
 ,若
,若 为函数
为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是
的图象是
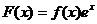 ,∴
,∴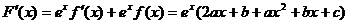 ,
, 为
为 的一个极值点,
的一个极值点, ,即
,即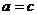 ,
, ,
, 时,
时, ,即对称轴所在直线方程为
,即对称轴所在直线方程为 ;
; 时,
时, ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.