网址:http://m.1010jiajiao.com/timu_id_12302[举报]
一、填空题(本大题满分48分,每小题4分,共12小题)
1..files\image179.gif) ; 2.
; 2..files\image181.gif) ; 3.
; 3..files\image183.gif) ; 4.
; 4..files\image185.gif) ; 5.
; 5..files\image187.gif) ;
;
6..files\image189.gif) ; 7.
; 7..files\image181.gif) ; 8.
; 8..files\image191.gif) ; 9.
; 9..files\image193.gif) ; 10.
; 10..files\image195.gif) ;
;
11..files\image197.gif) ; 12.
; 12..files\image199.gif) .
.
二、选择题(本大题满分16分,每小题4分,共4小题)
13.C; 14.A; 15.B; 16.C;
三、解答题(本大题满分86分,本大题共有6题)
17.(1).files\image201.gif) ;
;
.files\image203.gif)
(2).files\image205.gif) ;
; .files\image207.gif)
18.1号至4号正四棱柱形容器是体积依次为.files\image209.gif) 。
。
∵ .files\image110.gif) ,
,.files\image212.gif) ,
,
∴ 存在必胜方案,即选择3号和4号容器。
19.(1)∵ 由正弦定理,.files\image214.gif) ,∴
,∴ .files\image216.gif) ,
,.files\image218.gif) 。
。
∵ .files\image220.gif) , ∴
, ∴ .files\image222.gif) ,即
,即.files\image224.gif) 。∴
。∴ .files\image226.gif) 。
。
(2)∵ .files\image228.gif) ,
,
∴ .files\image230.gif) 。
。
20.(1)设放水.files\image125.gif) 分钟内水箱中的水量为
分钟内水箱中的水量为.files\image232.gif) 升
升
依题意得.files\image234.gif) ;
;
.files\image236.gif) 分钟时,水箱的水量
分钟时,水箱的水量.files\image238.gif) 升, 放水后
升, 放水后.files\image240.gif) 分钟水箱内水量接近最少;
分钟水箱内水量接近最少;
(2)该淋浴器一次有.files\image135.gif) 个人连续洗浴, 于是,
个人连续洗浴, 于是,.files\image243.gif) ,
,.files\image245.gif)
.files\image247.gif)
所以,一次可最多连续供7人洗浴。
21.(1)由.files\image249.gif) 及
及.files\image251.gif)
.files\image253.gif) ,∴
,∴.files\image255.gif) 时
时.files\image257.gif) 成等比数列。
成等比数列。
(2)因.files\image259.gif) ,由(1)知,
,由(1)知,.files\image261.gif) ,故
,故.files\image263.gif) 。
。
(3)设存在.files\image265.gif) ,使得
,使得.files\image267.gif) 成等差数列,则
成等差数列,则.files\image269.gif) ,
,
即.files\image271.gif)
.files\image273.gif) 因
因.files\image265.gif) ,所以
,所以.files\image275.gif) ,
,
∴不存在.files\image277.gif) 中的连续三项使得它们可以构成等差数列。
中的连续三项使得它们可以构成等差数列。
22.(1)解:设.files\image279.gif) 为函数
为函数.files\image281.gif) 图像的一个对称点,则
图像的一个对称点,则.files\image283.gif) 对于
对于.files\image285.gif) 恒成立.即
恒成立.即.files\image287.gif) 对于
对于.files\image285.gif) 恒成立,
恒成立,
.files\image289.gif) 由
由.files\image291.gif) ,故
,故.files\image293.gif) 图像的一个对称点为
图像的一个对称点为.files\image295.gif) .
.
(2)解:假设.files\image297.gif) 是函数
是函数.files\image299.gif) (
(.files\image301.gif) 的图像的一个对称点,
的图像的一个对称点,
则.files\image303.gif) (
(.files\image301.gif) 对于
对于.files\image285.gif) 恒成立,
恒成立,
即.files\image306.gif) 对于
对于.files\image285.gif) 恒成立,因为
恒成立,因为.files\image308.gif) ,所以
,所以.files\image306.gif) 不
不
恒成立,
即函数.files\image299.gif) (
(.files\image301.gif) 的图像无对称点.
的图像无对称点.
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组:![]() ;
;
第二组:![]() ;
;
(2)设![]() ,生成函数
,生成函数![]() .若不等式
.若不等式
![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,取
,取![]() ,生成函数
,生成函数![]() 图像的最低点坐标为
图像的最低点坐标为![]() .若对于任意正实数
.若对于任意正实数![]() 且
且![]() .试问是否存在最大的常数
.试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
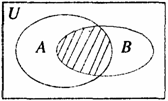
设函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,x0)为坐标的点为函数f(x)图像上的不动点.
(Ⅰ)若函数f(x)= 图像上有两点关于原点对称的不动点,求a、b应满足的条件;
图像上有两点关于原点对称的不动点,求a、b应满足的条件;
(Ⅱ)在(Ⅰ)的条件下,若a=8,记函数f(x)图像上的两个不动点分别为A、B,M为函数图像上的另一点,且其纵坐标yM>3,求点M到直线AB距离的最小值及取得最小值时M点的坐标;
(Ⅲ)下述命题“若定义在R上的奇函数f(x)图像上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举一反例说明.
查看习题详情和答案>>已知函数![]() 的周期为
的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数; 若不存在,说明理由.
的个数; 若不存在,说明理由.
(3)求实数![]() 与正整数
与正整数![]() ,使得
,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
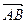 的坐标;
的坐标;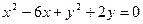 关于直线OB对称的圆的方程;
关于直线OB对称的圆的方程;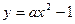 的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.