网址:http://m.1010jiajiao.com/timu_id_12106[举报]
说明:
1.本解答仅给出了一种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容对照评分标准制订相应的评分细则。
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数。
4.给分或扣分均以1分为单位,选择题和填空题不给中间分。
一.选择题:本题考查基本知识和基本运算
DDDBB;CDACA;CA
二.填空题:本题考查基本知识和基本运算
13.2; 14.  15. 2;
16. ①②③④
15. 2;
16. ①②③④
三.解答题:(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
解:(I)解:
 …………………………………………6分
…………………………………………6分
由
 ,得
,得 

 的单调递增区间为
的单调递增区间为

(II)
 的图象关于直线
的图象关于直线 对称,
对称,






18.(本小题满分12分)
解:(Ⅰ)当M是A
∵M为A
延长线交于N,则NC1=C
连结NB1并延长与CB延长线交于G,
则BG=CB,NB1=B
在△CGN中,BC1为中位线,BC1//GN.
又GN 平面MAB1,
平面MAB1,
∴BC1//平面MAB1 .………………………6分
(Ⅱ)∵BC1//平面MB
∵△AGC中, BC=BA=BG ,∴∠GAC=90°.
即AC⊥AG, 又AG⊥AA1 ,  ,
,
∴AG⊥平面A1ACC1.
∴ ,……………………………… 8分
,……………………………… 8分
∴∠MAC为平面MB

∴所求锐二面角大小为 . …………………………………………10分
. …………………………………………10分
(Ⅲ)设动点M到平面A1ABB1的距离为 ,
,
则 .当点M与点C1重合时,三棱锥B―AB
.当点M与点C1重合时,三棱锥B―AB …12分
…12分
19.(本小题满分12分)
解:设摇奖一次,获得一、二、三、四、五等奖的事件分别记为A,B,C,D,E。摇奖的概率大小与扇形区域 A,B,C,D,E所对应的圆心角大小成正比。
 ,
, 2分
2分
(1)摇奖两次,均获得一等奖的概率 ; 4分
; 4分
(2)购物满40元即可获得两次摇奖机会,所得的奖金数为 可以为2、3、4、5、6、7、8、9、10。从而有
可以为2、3、4、5、6、7、8、9、10。从而有
 7分
7分
所以 的分布列为:
的分布列为:

2
3
4
5
6
7
8
9
10










8分

10分
(3)由(2)知消费者刚好消费40元两次摇奖机会摇奖所得的平均奖数为4.63元;若选择让利获得的优惠为 ,显然4.63元
>4元。故选择摇奖比较划算。12分
,显然4.63元
>4元。故选择摇奖比较划算。12分
(文)解:设摇奖一次,获得一、二、三、四、五等奖的事件分别记为A,B,C,D,E。摇奖的概率大小与扇形区域 A,B,C,D,E所对应的圆心角大小成正比。 ,
, 3分
3分
(1)摇奖一次,至多获得三等奖的事件记为F,则 ; 即摇奖一次,至多获得三等奖的概率为
; 即摇奖一次,至多获得三等奖的概率为 ;
;
5分
(2)摇奖两次,均获得一等奖的概率 8分
8分
(3)购物满40元即可获得两次摇奖机会,由题意知,奖金数 的可能值为8、9、10。某消费者购物满40元,摇奖后奖金数不低于8元的事件记为G,则有
的可能值为8、9、10。某消费者购物满40元,摇奖后奖金数不低于8元的事件记为G,则有
 答:某消费者购物满40元,摇奖后奖金数不低于8元的概率为
答:某消费者购物满40元,摇奖后奖金数不低于8元的概率为 。12分
。12分
20.(本小题满分12分)
解:(Ⅰ)设 、
、 、
、 ,则
,则
 ,
,
由此及 得
得
 ,即
,即 ;
;
(Ⅱ)当 时,曲线
时,曲线 的方程为
的方程为 。
。
依题意,直线 和
和 均不可能与坐标轴平行,故不妨设直线
均不可能与坐标轴平行,故不妨设直线 (
( ),直线
),直线 ,从而有
,从而有
 。
。
同理,有 。
。
若 是等腰三角形,则
是等腰三角形,则 ,由此可得
,由此可得
 ,即
,即 或
或 。
。
下面讨论方程 的根的情形(
的根的情形( ):
):
①若 ,则
,则 ,方程没有实根;
,方程没有实根;
②若 ,则
,则 ,方程有两个相等的实根
,方程有两个相等的实根 ;
;
③若 ,则
,则 ,方程有两个相异的正实根,且均不等于
,方程有两个相异的正实根,且均不等于 (因为
(因为
 )。
)。
综上所述, 能是等腰三角形:当
能是等腰三角形:当 时,这样的三角形有且仅有一个;而当
时,这样的三角形有且仅有一个;而当 时,这样的三角形有且仅有三个。
时,这样的三角形有且仅有三个。
21.解:(I) ………………2分
………………2分


 当
当 或
或 时,
时, ;当
;当 时,
时,
 在
在 ,(1,
,(1, 内单调递增,在
内单调递增,在 内单调递减…………4分
内单调递减…………4分
故 的极小值为
的极小值为 ……………………………………5分
……………………………………5分
(II)①若 则
则
 的图象与
的图象与 轴只有一个交点。……6分
轴只有一个交点。……6分
②若 则
则 ,
, 当
当 时,
时, ,当
,当 时,
时,
 的极大值为
的极大值为
 的极小值为
的极小值为
 的图象与
的图象与 轴有三个公共点。
轴有三个公共点。
③若 ,则
,则 。
。
 当
当 时,
时, ,当
,当 时,
时,
 的图象与
的图象与 轴只有一个交点
轴只有一个交点
④若 ,则
,则
 的图象与
的图象与 轴只有一个交点
轴只有一个交点
⑤当 ,由(I)知
,由(I)知 的极大值为
的极大值为
综上所述,若
 的图象与
的图象与 轴只有一个公共点;
轴只有一个公共点;
若 ,
, 的图象与
的图象与 轴有三个公共点。
轴有三个公共点。
22.(本小题满分14分)
解:(Ⅰ)∵第n个集合有n个奇数,∴在前n个集合中共有奇数的个数为
 .…………………………………… 2分
.…………………………………… 2分
则第n个集合中最大的奇数 =
= .………………4分
.………………4分
(Ⅱ)(i)由(Ⅰ)得 ,
,
从而得 .……………………………………6分
.……………………………………6分
(ii)由(i)得 , ∴
, ∴
 .…7分
.…7分
(1)当 时,
时, ,显然2≤
,显然2≤ .……………………………………8分
.……………………………………8分
(2)当 ≥2 时,
≥2 时, ………9分
………9分
> ,……………………………………………10分
,……………………………………………10分

≤ .………………………………………………12分
.………………………………………………12分
∴
<
 .即
.即 .
.
综上所述,2≤ . ……………………………………………………14分
. ……………………………………………………14分
过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 直线
直线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() 直线
直线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]()
(1)当△AOB的面积达到最大值时,求四边形AOBM外接圆方程;
(2)若直线![]() 将四边形
将四边形![]() 分割成面积相等的两部分,求△AOB的面积
分割成面积相等的两部分,求△AOB的面积
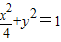 的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.(1)当直线AM的斜率为1时,求点M的坐标;
(2)当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点,若不过定点,请说明理由.
查看习题详情和答案>>
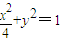 的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.(1)当直线AM的斜率为1时,求点M的坐标;
(2)当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点,若不过定点,请说明理由.
查看习题详情和答案>>