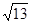题目内容
已知椭圆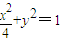 的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.(1)当直线AM的斜率为1时,求点M的坐标;
(2)当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点,若不过定点,请说明理由.
【答案】分析:(1)根据直线AM的斜率为1时,得出直线AM:y=x+2,代入椭圆方程并化简得:5x2+16x+12=0,解得点M的坐标即可;(2)对于是否过x轴上的一定点问题,可先假设存在,设直线AM的斜率为k,则AM:y=k(x+2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系即可求得P点的坐标,从而解决问题.
解答:解:(1)直线AM的斜率为1时,直线AM:y=x+2,(1分)
代入椭圆方程并化简得:5x2+16x+12=0,(2分)
解之得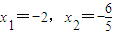 ,∴
,∴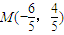 .(4分)
.(4分)
(2)设直线AM的斜率为k,则AM:y=k(x+2),
则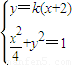 化简得:(1+4k2)x2+16k2x+16k2-4=0.(6分)
化简得:(1+4k2)x2+16k2x+16k2-4=0.(6分)
∵此方程有一根为-2,∴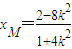 ,(7分)
,(7分)
同理可得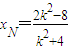 .(8分)
.(8分)
由(1)知若存在定点,则此点必为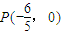 .(9分)
.(9分)
∵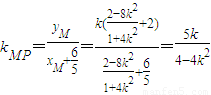 ,(11分)
,(11分)
同理可计算得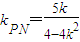 .(13分)
.(13分)
∴直线MN过x轴上的一定点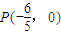 .(16分)
.(16分)
点评:本题考查直接法求轨迹方程、直线与抛物线的位置关系、直线过定点问题.考查推理能力和运算能力.
解答:解:(1)直线AM的斜率为1时,直线AM:y=x+2,(1分)
代入椭圆方程并化简得:5x2+16x+12=0,(2分)
解之得
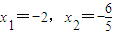 ,∴
,∴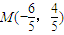 .(4分)
.(4分)(2)设直线AM的斜率为k,则AM:y=k(x+2),
则
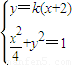 化简得:(1+4k2)x2+16k2x+16k2-4=0.(6分)
化简得:(1+4k2)x2+16k2x+16k2-4=0.(6分)∵此方程有一根为-2,∴
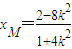 ,(7分)
,(7分)同理可得
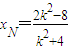 .(8分)
.(8分)由(1)知若存在定点,则此点必为
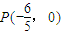 .(9分)
.(9分)∵
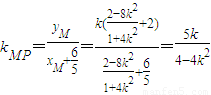 ,(11分)
,(11分)同理可计算得
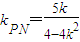 .(13分)
.(13分)∴直线MN过x轴上的一定点
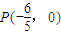 .(16分)
.(16分)点评:本题考查直接法求轨迹方程、直线与抛物线的位置关系、直线过定点问题.考查推理能力和运算能力.

练习册系列答案
相关题目
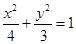 的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当
的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当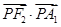 取最小值时,
取最小值时,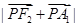 的值为( )
的值为( )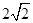 B、3 C、
B、3 C、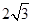 D、
D、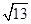
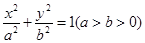 的左顶点为
的左顶点为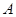 ,左焦点为
,左焦点为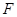 ,上顶点为
,上顶点为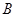 ,若
,若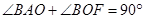 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .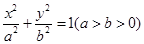 的左顶点为
的左顶点为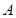 ,左焦点为
,左焦点为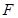 ,上顶点为
,上顶点为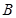 ,若
,若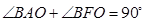 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.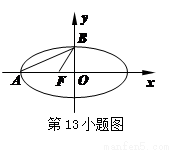
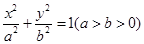 的左顶点为
的左顶点为 ,左焦点为
,左焦点为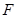 ,上顶点为
,上顶点为 ,若
,若 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.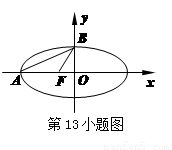
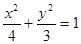 的左顶点为
的左顶点为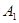 ,右焦点为
,右焦点为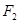 ,点
,点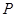 为该椭圆上一动点,则当
为该椭圆上一动点,则当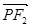
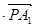 取最小值时,
取最小值时,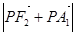 的值为
( )
的值为
( )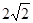 B.
B.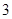 C.
C. 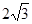 D.
D.