网址:http://m.1010jiajiao.com/timu_id_12032[举报]
一、选择题:(本大题共10小题,每小题5分,共50分)
1 B
B  A 3
A 3 文C(理C) 4
文C(理C) 4 D 5
D 5 文A(理B) 6
文A(理B) 6 文B(理C) 7
文B(理C) 7 文C(理C) 8
文C(理C) 8 文C(理A) 9
文C(理A) 9 文A (理D) 10
文A (理D) 10 文D(理A)
文D(理A)
 三、解答题:(本大题共6个解答题,满分76分,)
三、解答题:(本大题共6个解答题,满分76分,)
线为y轴建立平面直角坐标系如图所示,
则A(-4,0),N(4,0),设P(x,y) 
由|PM|:|PN|= ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:


代入坐标得:

整理得:
即

所以动点P的轨迹是以点


(理)解:(I)当a=1时 



 或
或 或
或

 或
或

(II)原不等式
设 有
有

当且仅当
即 时
时



解得








若由方程组 解得
解得 ,可参考给分
,可参考给分
(理)解:(Ⅰ)设 (a≠0),则
(a≠0),则
 …… ①
…… ①
 …… ②
…… ②
又∵ 有两等根
有两等根
∴ …… ③
…… ③
由①②③得

又∵

∴a<0, 故
∴

(Ⅱ)


∵g(x)无极值
∴方程

得



 或
或 或
或

 或
或

(II)原不等式
设 有
有

当且仅当
即 时
时

(理)解:以AN所在直线为x轴,AN的中垂
线为y轴建立平面直角坐标系如图所示,
则A(-4,0),N(4,0),设P(x,y) 
由|PM|:|PN|= ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:


代入坐标得:

整理得:
即

所以动点P的轨迹是以点


 …… ①
…… ①
 …… ②
…… ②
又∵ 有两等根
有两等根
∴ …… ③
…… ③
由①②③得

又∵

∴a<0, 故
∴

(Ⅱ)


∵g(x)无极值
∴方程

得

(理)解:(I)设 (1)
(1)
又 故
故 (2)
(2)
由(1),(2)解得

(II)由向量 与向量
与向量 的夹角为
的夹角为 得
得
由 及A+B+C=
及A+B+C= 知A+C=
知A+C=
则






由0<A< 得
得 ,得
,得
故 的取值范围是
的取值范围是

Sn+1=2an+1-3(n+1),两式相减并整理得:an+1=2an+3

所以3+ an+1=2(3+an),又a1=S1=2a1-3,a1=3可知3+
a1=6 ,进而可知an+3
,进而可知an+3
所以 ,故数列{3+an}是首相为6,公比为2的等比数列,
,故数列{3+an}是首相为6,公比为2的等比数列,
所以3+an=6 ,即an=3(
,即an=3( )
)
 12、已知函数f(x)是定义在R上的函数,如果函数f(x)在R上的导函数f′(x)的图象如图,则有以下几个命题:
12、已知函数f(x)是定义在R上的函数,如果函数f(x)在R上的导函数f′(x)的图象如图,则有以下几个命题:(1)f(x)的单调递减区间是(-2,0)、(2,+∞),f(x)的单调递增区间是(-∞,-2)、(0,2);
(2)f(x)只在x=-2处取得极大值;
(3)f(x)在x=-2与x=2处取得极大值;
(4)f(x)在x=0处取得极小值.
其中正确命题的个数为( )
已知函数f(x)是定义在R上的函数,如果函数f(x)在R上的导函数f′(x)的图象如图,则有以下几个命题:
(1)f(x)的单调递减区间是(-2,0)、(2,+∞),f(x)的单调递增区间是(-∞,-2)、(0,2);
(2)f(x)只在x=-2处取得极大值;
(3)f(x)在x=-2与x=2处取得极大值;
(4)f(x)在x=0处取得极小值.
其中正确命题的个数为 ( )
| A.1 | B.2 |
| C.3 | D.4 |
已知函数f(x)是定义在R上的函数,如果函数f(x)在R上的导函数f′(x)的图象如图,则有以下几个命题:
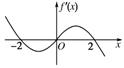
(1)f(x)的单调递减区间是(-2,0)、(2,+∞),f(x)的单调递增区间是(-∞,-2)、(0,2);
(2)f(x)只在x=-2处取得极大值;
(3)f(x)在x=-2与x=2处取得极大值;
(4)f(x)在x=0处取得极小值.
其中正确命题的个数为 ( )
A.1 B.2
C.3 D.4
查看习题详情和答案>>
 ,则
,则 ” ,(理)
” ,(理)
 ,(理)
,(理) ,
,  16
16 为所求
为所求