网址:http://m.1010jiajiao.com/timu_id_11913[举报]
一、1. A 2.B 3.B 4.C 5.A 6.D 7.A 8.C 9.B 10.A 11.D 12.D
二、13.1 14.1 15.r≥6 16.81
三、
 18. (1)设 A为
“甲预报站预报准确”B为“乙预报站预报准确”则在同一时间段里至少
18. (1)设 A为
“甲预报站预报准确”B为“乙预报站预报准确”则在同一时间段里至少
有一个预报准确的概率为 -------4分
-------4分
(2)①
 的分布列为
的分布列为

0
1
2
3
p
0.008
0.096
0.384
0.512
 分
分
②由 在
在 上的值恒为正值得
上的值恒为正值得

 ---12分
---12分
19. 解法一
(1)证明:连AC交DB于点O,
由正四棱柱性质可知AA1⊥底面ABCD,AC⊥BD,∴A
又∵A1B1⊥侧面BC1且BC1⊥BE ∴A
又∵BD∩BE=B,∴A
(2)设A
在侧面BC1中,BE⊥B
∴ 又BC=2,BB1=4,∴CE=1.
又BC=2,BB1=4,∴CE=1.
连OE,则OE为平面ACC
在RtㄓECO中, ,∴
,∴
又 ∵
∵
又 ,∴
,∴ 在RtㄓA1BK中,
在RtㄓA1BK中, ,即为A1B与平面BDE所成的角的正弦值.
,即为A1B与平面BDE所成的角的正弦值.
解法二:
(1) 以D为原点,DA、DC、DD1所在的直线分别为x,y,z轴建立空间直角坐标系 .
.
D(0,0,0), A(2,0,0),B(2,2,0),C(0,2,0)
A1(2,0,4),B1(2,2,4),C1(0,2,4),D1(0,0,4),设点E(0,2,t)
∵BE⊥B
 ,∴E(0,2,1)
,∴E(0,2,1)
又 ,
, ,
,
∴
∴A
(2)设A
则
∴ ∴
∴
由 ⊥
⊥  得
得
∴ ,…………①
,…………①
 同理有
同理有
 得
得
…②
由①②联立,解得 ∴
∴
∴ ,又易知
,又易知
∴ ,即所求角的正弦值为
,即所求角的正弦值为 .
.
20.解:(1)易得 .
.
(2)设P 为
为 的图像上任一点,点P关于直线
的图像上任一点,点P关于直线 的对称点为
的对称点为
∵点 在
在 的图像上,
的图像上,
∴ ,即得
,即得 .
.
(3)
 下面求
下面求 的最小值:
的最小值:
①当 ,即
,即 时
时
由 ,得
,得 ,所以
,所以 .
.
②当 即
即 时
时 在R上是增函数,无最小值,与
在R上是增函数,无最小值,与 不符.
不符.
③当 即
即 时,
时, 在R上是减函数,无最小值,与
在R上是减函数,无最小值,与 不符.
不符.
④当 即
即 时,
时, ,与最小值
,与最小值 不符.
不符.
综上所述,所求 的取值范围是
的取值范围是 .
.
21.(1)解:设P(a,0),Q(0,b)则: ∴
∴
设M(x,y)∵ ∴
∴
 ∴
∴
(2)解法一:设A(a,b), ,
, (x1≠x2)
(x1≠x2)
则直线SR的方程为: ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
对 求导得:y′=
求导得:y′= x
x
∴抛物线上S.R处的切线方程为
 即4
即4 ②
②
 即4
即4 ③
③
联立②、③得 
代入①得:ax-2y-2b=0故:B点在直线ax-2y-2b=0上.
解法二:设A(a,b),当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a).
与 联立消去y,得x2-4kx+4ak-4b=0.设
联立消去y,得x2-4kx+4ak-4b=0.设 ,
, (x1≠x2)
(x1≠x2)
则由韦达定理,得
又过S、R点的切线方程分别为 ,
, .
.
联立,并解之,得 (k为参数) 消去k,得ax-2y-2b=0.
(k为参数) 消去k,得ax-2y-2b=0.
故B点在直线2ax-y-b=0上.
22.解:(1) =22;
=22;


(3)由(2)知

 =
=

 .
.
| 1 | anan+1 |
(1)求数列{an}的通项公式;
(2)若S2为S1,Sm (m∈N*)的等比中项,求正整数m的值.
(3)对任意正整数k,将等差数列{an}中落入区间(2k,22k)内项的个数记为ck,求数列{cn}的前n项
和Tn.
xn+[
| ||
| 2 |
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>
| a |
④对某个正整数k,若xk+1≥xk,则xk=[
| a |
其中的真命题有
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.
①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
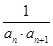 ,其前n项和为Sn.
,其前n项和为Sn.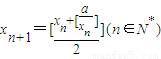 ,现有下列命题:
,现有下列命题: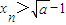 ;
; .
.