题目内容
记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,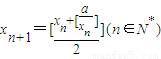 ,现有下列命题:
,现有下列命题:①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,
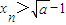 ;
;④对某个正整数k,若xk+1≥xk,则
 .
.其中的真命题有 .(写出所有真命题的编号)
【答案】分析:按照给出的定义对四个命题结合数列的知识逐一进行判断真假,①列举即可;②需举反例;③可用数学归纳法加以证明;④可由归纳推理判断其正误
解答:解:①当a=5时,x1=5,
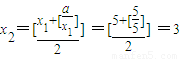 ,
,
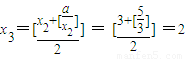 ,
,
∴①正确.
②当a=8时,x1=8,
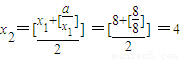
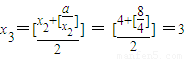
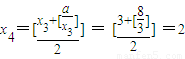

∴此数列从第三项开始为3,2,3,2,3,2…为摆动数列,故②错误;
③当n=1时,x1=a,∵a-(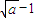 )=
)=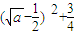 >0,∴x1=a>
>0,∴x1=a>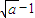 成立,
成立,
假设n=k时,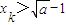 ,
,
则n=k+1时,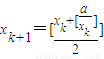 ,
,
∵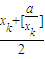 ≥
≥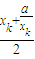 ≥
≥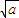 ,
,
∴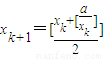 >
>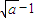
∴对任意正整数n,当n≥1时,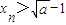 ;③正确;
;③正确;
④∵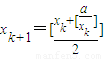 ≥xk,
≥xk,
由数列①②规律可知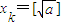 一定成立
一定成立
故正确答案为①③④
点评:本题主要考查了数列递推公式的应用,归纳推理和演绎推理的方法,直接证明和间接证明方法,数学归纳法的应用,难度较大,需有较强的推理和思维能力
解答:解:①当a=5时,x1=5,
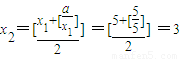 ,
,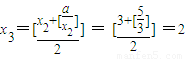 ,
,∴①正确.
②当a=8时,x1=8,
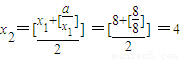
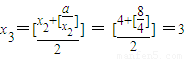
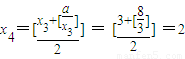

∴此数列从第三项开始为3,2,3,2,3,2…为摆动数列,故②错误;
③当n=1时,x1=a,∵a-(
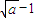 )=
)=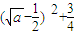 >0,∴x1=a>
>0,∴x1=a>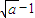 成立,
成立,假设n=k时,
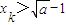 ,
,则n=k+1时,
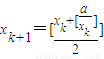 ,
,∵
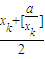 ≥
≥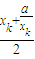 ≥
≥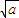 ,
,∴
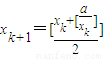 >
>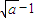
∴对任意正整数n,当n≥1时,
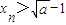 ;③正确;
;③正确;④∵
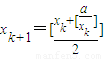 ≥xk,
≥xk,由数列①②规律可知
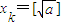 一定成立
一定成立故正确答案为①③④
点评:本题主要考查了数列递推公式的应用,归纳推理和演绎推理的方法,直接证明和间接证明方法,数学归纳法的应用,难度较大,需有较强的推理和思维能力

练习册系列答案
相关题目
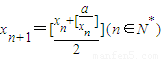 ,现有下列命题:
,现有下列命题: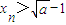 ;
;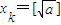 .
.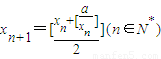 ,现有下列命题:
,现有下列命题: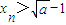 ;
;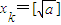 .
. ,现有下列命题:
,现有下列命题: ;
; .
.