摘要:(1)若补充地球表面的重力加速度g,可以认为热气球受到的万有引力近似等于其重力.则有
网址:http://m.1010jiajiao.com/timu_id_118881[举报]
I、正在修建的房顶上固定的根不可伸长的细线垂到三楼窗沿下,某同学应用单摆原理测量窗的上沿到房顶的高度,先将线的下端系上一个小球.发现当小球静止时,细线恰好与窗子上沿接触且保持竖直.他打开窗子,让小球在垂直于窗子的竖直平面内摆动,如图1.测量周期时计时起点应选择小球通过图中的

II、某同学设计了如图2的电路,用来测量未知电阻Rx的阻值,在下列可供选择的器材中:
A.被测电阻Rx,阻值约为50Ω
B.电源(电动势10V,内阻0.5Ω)
C.电流表(量程0-200mA,内阻r2)
D.电流表(量程0-300mA,内阻约为r3)
E.定值电阻500Ω
F.定值电阻100Ω
G.滑动变阻器(0-100Ω,1A)
H.滑动变阻器(0-2000Ω,0.5A)
I.电键,导线若干
测量时,为使结果尽可能精确,电路安全,电流表A1应选用
将该同学的实验步骤补充完整:
①将滑动变阻器的滑片移到最右端,闭合电键;
②将滑动变阻器的滑片移到适当位置,读出电流表A1、A2的读数;
③
④实验完毕后,拆除电路.
若某次测量时电流表A1、A2的读数分别为I1、I2,则被测电阻的测量值为Rx=
-r2
-r2.
查看习题详情和答案>>
B
B
点最为合理(用图中字母表示).该同学测得小球运动的周期T=3s,球在最低点B时球心到窗上沿的距离为1m,则房顶到窗上沿的高度h3
3
m.(地重力加速度g取π2m/s2).
II、某同学设计了如图2的电路,用来测量未知电阻Rx的阻值,在下列可供选择的器材中:
A.被测电阻Rx,阻值约为50Ω
B.电源(电动势10V,内阻0.5Ω)
C.电流表(量程0-200mA,内阻r2)
D.电流表(量程0-300mA,内阻约为r3)
E.定值电阻500Ω
F.定值电阻100Ω
G.滑动变阻器(0-100Ω,1A)
H.滑动变阻器(0-2000Ω,0.5A)
I.电键,导线若干
测量时,为使结果尽可能精确,电路安全,电流表A1应选用
C
C
,电流表A2应选用D
D
,R1应选用F
F
,R2应选用G
G
.(填所选仪器前面的字母)将该同学的实验步骤补充完整:
①将滑动变阻器的滑片移到最右端,闭合电键;
②将滑动变阻器的滑片移到适当位置,读出电流表A1、A2的读数;
③
再移动滑片,读出几组A1、A2的读数,算出对应的Rx值,求出平均值
再移动滑片,读出几组A1、A2的读数,算出对应的Rx值,求出平均值
;④实验完毕后,拆除电路.
若某次测量时电流表A1、A2的读数分别为I1、I2,则被测电阻的测量值为Rx=
| (I2-I1)R1 |
| I1 |
| (I2-I1)R1 |
| I1 |
某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即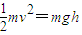 .直接测量摆球到达B点的速度v比较困难.现让小球在B点处脱离悬线做平抛运动,利用平抛的特性来间接地测出v.如图(a)中,悬点正下方P点处放有水平放置炽热的电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出作平抛运动.实验步骤如下(将下列实验步骤补充完整,自己设定需用的字母):
.直接测量摆球到达B点的速度v比较困难.现让小球在B点处脱离悬线做平抛运动,利用平抛的特性来间接地测出v.如图(a)中,悬点正下方P点处放有水平放置炽热的电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出作平抛运动.实验步骤如下(将下列实验步骤补充完整,自己设定需用的字母):
(1)在地面上放上白纸,上面覆盖着复写纸,当小球落在复写纸上时,会在下面白纸上留下痕迹.
(2)用重锤线确定出A、B点的投影点N、M.
(3)让小球每一次都______释放,重复实验10次.球的落点痕迹如图(b)所示,图中米尺水平放置,零刻度线与M点对齐.
(4)用米尺量出______,算出A、B两点的竖直距离,再量出______,即可验证机械能守恒定律.已知重力加速度为g,小球的质量为m.
(5)数据处理
①根据图(b)可以确定小球平抛时的水平射程为______cm.
②表示出小球平抛时的初速度v=______
 查看习题详情和答案>>
查看习题详情和答案>>
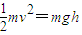 .直接测量摆球到达B点的速度v比较困难.现让小球在B点处脱离悬线做平抛运动,利用平抛的特性来间接地测出v.如图(a)中,悬点正下方P点处放有水平放置炽热的电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出作平抛运动.实验步骤如下(将下列实验步骤补充完整,自己设定需用的字母):
.直接测量摆球到达B点的速度v比较困难.现让小球在B点处脱离悬线做平抛运动,利用平抛的特性来间接地测出v.如图(a)中,悬点正下方P点处放有水平放置炽热的电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出作平抛运动.实验步骤如下(将下列实验步骤补充完整,自己设定需用的字母):(1)在地面上放上白纸,上面覆盖着复写纸,当小球落在复写纸上时,会在下面白纸上留下痕迹.
(2)用重锤线确定出A、B点的投影点N、M.
(3)让小球每一次都______释放,重复实验10次.球的落点痕迹如图(b)所示,图中米尺水平放置,零刻度线与M点对齐.
(4)用米尺量出______,算出A、B两点的竖直距离,再量出______,即可验证机械能守恒定律.已知重力加速度为g,小球的质量为m.
(5)数据处理
①根据图(b)可以确定小球平抛时的水平射程为______cm.
②表示出小球平抛时的初速度v=______
 查看习题详情和答案>>
查看习题详情和答案>>
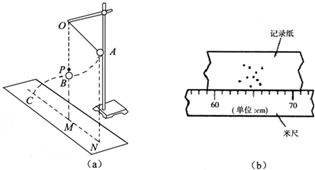 某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即
某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即| 1 |
| 2 |
(1)在地面上放上白纸,上面覆盖着复写纸,当小球落在复写纸上时,会在下面白纸上留下痕迹.
(2)用重锤线确定出A、B点的投影点N、M.
(3)让小球每一次都
同一点由静止
同一点由静止
释放,重复实验10次.球的落点痕迹如图(b)所示,图中米尺水平放置,零刻度线与M点对齐.(4)用米尺量出
AN的高度h1、BM的高度h2,
AN的高度h1、BM的高度h2,
,算出A、B两点的竖直距离,再量出M、C之间的距离x
M、C之间的距离x
,即可验证机械能守恒定律.已知重力加速度为g,小球的质量为m.(5)数据处理
①根据图(b)可以确定小球平抛时的水平射程为
65.0
65.0
cm.②表示出小球平抛时的初速度v0=
x.
|
x.
.(用题中所给字母和自己设定的字母表示)
|
③用测出的物理量表示出小球从A到B过程中,重力势能的减少量△EP=
mg(h1-h2)
mg(h1-h2)
,动能的增加量△EK=| mgx2 |
| 4h2 |
| mgx2 |
| 4h2 |
④本实验误差的主要来源有
小球在运动过程中受到阻力
小球在运动过程中受到阻力
(试举出一条).“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为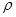 ;石油密度远小于
;石油密度远小于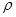 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。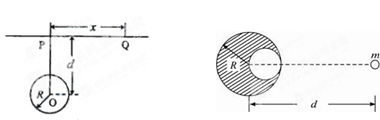
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径), =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为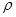 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力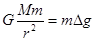 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值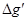 (
(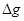 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在 与
与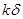 (k>1)(
(k>1)( 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为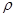 ;石油密度远小于
;石油密度远小于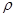 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。

(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径),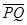 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为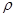 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力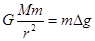 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值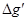 (
(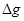 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在 与
与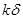 (k>1)(
(k>1)( 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
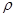 ;石油密度远小于
;石油密度远小于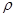 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径),
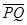 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为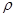 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力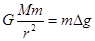 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值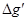 (
(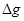 在OP方向上的分量)
在OP方向上的分量)(3)若在水平地面上半径L的范围内发现:重力加速度反常值在
 与
与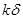 (k>1)(
(k>1)( 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。