摘要：由题意.得A,. -
网址：http://m.1010jiajiao.com/timu_id_11775[举报]
注意：第（3）小题平行班学生不必做，特保班学生必须做．
已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率e=
，过椭圆的右焦点F作与坐标轴不垂直的直线l，交椭圆于A、B两点．
（1）求椭圆的标准方程；
（2）设点M（m，0）是线段OF上的一个动点，且(
+
)⊥
，求m的取值范围；
（3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．
查看习题详情和答案>>
已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率e=
| 2 | ||
|
（1）求椭圆的标准方程；
（2）设点M（m，0）是线段OF上的一个动点，且(
| MA |
| MB |
| AB |
（3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．
注意：第（3）小题平行班学生不必做，特保班学生必须做．
已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率
，过椭圆的右焦点F作与坐标轴不垂直的直线l，交椭圆于A、B两点．
（1）求椭圆的标准方程；
（2）设点M（m，0）是线段OF上的一个动点，且
，求m的取值范围；
（3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．
查看习题详情和答案>>
已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率
，过椭圆的右焦点F作与坐标轴不垂直的直线l，交椭圆于A、B两点．（1）求椭圆的标准方程；
（2）设点M（m，0）是线段OF上的一个动点，且
，求m的取值范围；（3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．
查看习题详情和答案>>
（1）椭圆C：
（a>b>0）与x轴交于A、B两点，点P是椭圆C上异于A、B的任意一点，直线PA、 PB分别与y轴交于点M、N，求证：
为定值
．
（2）由（1）类比可得如下真命题：双曲线C：
（a>0，b>0）与x轴交于A、B两点，点P是双曲线C上异于A、B的任意一点，直线PA、PB分别与y轴交于点M、N，求证：为定值．请写出这个定值（不要求给出解题过程）．
（1）椭圆C：
（a>b>0）与x轴交于A、B两点，点P是椭圆C上异于A、B的任意一点，直线PA、 PB分别与y轴交于点M、N，求证：
为定值
．
（2）由（1）类比可得如下真命题：双曲线C：
（a>0，b>0）与x轴交于A、B两点，点P是双曲线C上异于A、B的任意一点，直线PA、PB分别与y轴交于点M、N，求证：为定值．请写出这个定值（不要求给出解题过程）．
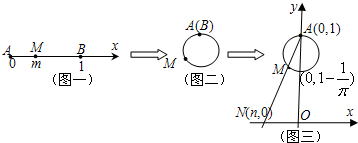如图揭示了一个由区间（0，1）到实数集R上的对应过程：区间（0，1）内的任意实数m与数轴上的线段AB（不包括端点）上的点M一一对应（图一），将线段AB围成一个圆，使两端A，B恰好重合（图二），再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1）（图三）．图三中直线AM与x轴交于点N（n，0），由此得到一个函数n=f（m），则下列命题中正确的序号是（ ）（1）f（
| 1 |
| 2 |
（2）f（x）是偶函数；
（3）f（x）在其定义域上是增函数；
（4）y=f（x）的图象关于点（
| 1 |
| 2 |
| A、（1）（3）（4） |
| B、（1）（2）（3） |
| C、（1）（2）（4） |
| D、（1）（2）（3）（4） |