摘要:C.D到平面的距离为1.2.同理可得B到平面的距离为1,所以选①③.已知(Ⅰ)求的值,(Ⅱ)求的值.解:(Ⅰ)由.得.所以=.(Ⅱ)∵.∴.在添加剂的搭配使用中.为了找到最佳的搭配方案.需要对各种不同的搭配方式作比较.在试制某种牙膏新品种时.需要选用两种不同的添加剂.现有芳香度分别为0.1.2.3.4.5的六种添加剂可供选用.根据试验设计原理.通常首先要随机选取两种不同的添加剂进行搭配试验.(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率,(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率,解:设“所选用的两种不同的添加剂的芳香度之和等于4 的事件为A.“所选用的两种不同的添加剂的芳香度之和不小于3 的事件为B (Ⅰ)芳香度之和等于4的取法有2种:..故.(Ⅱ)芳香度之和等于1的取法有1种:,芳香度之和等于2的取法有1种:.故.如图.P是边长为1的正六边形ABCDEF所在平面外一点..P在平面ABC内的射影为BF的中点O.(Ⅰ)证明⊥,(Ⅱ)求面与面所成二面角的大小.解:(Ⅰ)在正六边形ABCDEF中.为等腰三角形.∵P在平面ABC内的射影为O.∴PO⊥平面ABF.∴AO为PA在平面ABF内的射影,∵O为BF中点.∴AO⊥BF.∴PA⊥BF.(Ⅱ)∵PO⊥平面ABF.∴平面PBF⊥平面ABC,而O为BF中点.ABCDEF是正六边形 .∴A.O.D共线.且直线AD⊥BF.则AD⊥平面PBF,又∵正六边形ABCDEF的边长为1.∴...过O在平面POB内作OH⊥PB于H.连AH.DH.则AH⊥PB.DH⊥PB.所以为所求二面角平面角.在中.OH=.=.在中.,而(Ⅱ)以O为坐标原点.建立空间直角坐标系.P.B.∴..设平面PAB的法向量为.则..得.,设平面PDB的法向量为.则..得.,设函数.已知是奇函数.(Ⅰ)求.的值.(Ⅱ)求的单调区间与极值.证明(Ⅰ)∵.∴.从而=是一个奇函数.所以得.由奇函数定义得,知.从而.由此可知.和是函数是单调递增区间,是函数是单调递减区间,在时.取得极大值.极大值为.在时.取得极小值.极小值为.在等差数列中..前项和满足条件. (Ⅰ)求数列的通项公式,(Ⅱ)记.求数列的前项和.解:(Ⅰ)设等差数列的公差为,由得:.所以.即.又=.所以.(Ⅱ)由.得.所以.当时.,当时..即.如图.F为双曲线C:的右焦点.P为双曲线C右支上一点.且位于轴上方.M为左准线上一点.为坐标原点.已知四边形为平行四边形.. (Ⅰ)写出双曲线C的离心率与的关系式,(Ⅱ)当时.经过焦点F且平行于OP的直线交双曲线于A.B点.若.求此时的双曲线方程.解:∵四边形是.∴.作双曲线的右准线交PM于H.则.又..(Ⅱ)当时....双曲线为.设P.则..所以直线OP的斜率为.则直线AB的方程为.代入到双曲线方程得:.又.由得:.解得.则.所以为所求.
网址:http://m.1010jiajiao.com/timu_id_11549[举报]
(理科)在平面直角坐标系中,F为抛物线C:x2=2py(p>0)的焦点,M为抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M;若不存在,说明理由.
(3)若点M的横坐标为2,直线l:y=kx+
与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
查看习题详情和答案>>
| 3 |
| 4 |
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M;若不存在,说明理由.
(3)若点M的横坐标为2,直线l:y=kx+
| 1 |
| 4 |
(理科)在平面直角坐标系中,F为抛物线C:x2=2py(p>0)的焦点,M为抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M;若不存在,说明理由.
(3)若点M的横坐标为2,直线l:y=kx+ 与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
查看习题详情和答案>>
(理科)在平面直角坐标系中,F为抛物线C:x2=2py(p>0)的焦点,M为抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M;若不存在,说明理由.
(3)若点M的横坐标为2,直线l:y=kx+ 与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
查看习题详情和答案>>
 .
.(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M;若不存在,说明理由.
(3)若点M的横坐标为2,直线l:y=kx+
 与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.查看习题详情和答案>>
 .
. 与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.
与抛物线C有两个不同的交点A、B,l与圆Q有两个不同的交点D、E,用含k的式子表示 AB2+DE2.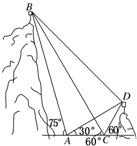 如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,
如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,