摘要： A是由定义在上且满足如下条件的函数组成的集合:①对任意.都有 , ②存在常数.使得对任意的.都有(Ⅰ)设.证明:(Ⅱ)设,如果存在,使得,那么这样的是唯一的;(Ⅲ)设,任取,令证明:给定正整数k,对任意的正整数p,成立不等式解:对任意,,,,所以对任意的...所以0<,令=..所以反证法:设存在两个使得,则由.得.所以.矛盾.故结论成立..所以+-
网址：http://m.1010jiajiao.com/timu_id_11475[举报]
（本小题满分12分）
已知函数f（x）是定义在[-e,0）∪（0,e]上的奇函数，当x∈（0,e],f（x）=ax+lnx（其中e是自然对数的底数，a∈R）
（1）求f（x）的解析式；
（2）设g（x）=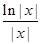
,x∈[-e,0）,求证：当a=-1时，f（x）>g（x）+
;
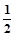（3）是否存在实数a，使得当x∈[-e,0）时f（x）的最小值是3 如果存在，求出实数a的值；如果不存在，请说明理由．
查看习题详情和答案>>
（本小题满分12分）设函数
（Ⅰ）当a=0时，
在（1,+∞）上恒成立，求实数
的取值范围;
（Ⅱ）当=2时，若函数
在［1,3］上恰有两个不同零点，求实数
的取值范围;
（Ⅲ）是否存在实数，使函数f(x)和函数h(x)在公共定义域上具有相同的单调性？若存在，求出的值，若不存在，说明理由。
(本小题满分12分)已知f(x)=ex-ax-1.
（1）求f(x)的单调增区间；
（2）若f(x）在定义域R内单调递增，求a的取值范围；
（3）是否存在a,使f(x)在（-∞，0］上单调递减，在［0，+∞）上单调递增？若存在，求出a的值；若不存在，说明理由.