摘要:3.在一根长为0.2m的直导线中通入2A的电流.将此通电导线放在磁感应强度为0.5T的匀强磁场中.则导线受到的安培力的大小可能是
网址:http://m.1010jiajiao.com/timu_id_1088616[举报]
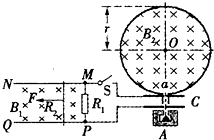 如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:(1)5s末电阻R1上消耗的电功率.
(2)5s末外力F的功率
(3)若杆最终以8m/s的速度做匀速运动,此时闭合电键S,α射线源A释放的α粒子经加速电场C加速后从 a 孔对着圆心0进入半径r=
| 3 |
| 6.4 |
| 6.6 |
如图所示(俯视),MN和PQ是两根固定在同一水平面上的足够长且电阻不计的平行金属导轨,两导轨间距L=0.2m,其间有一个方向垂直水平面竖直向下的匀强磁场B1=5.0T.导轨上NQ之间接一电阻R1=0.40Ω,阻值为R2=0.10Ω的金属杆垂直导轨放置并与导轨始终保持良好接触.两导轨右端通过金属导线分别与电容器C的两极相连.电容器C紧挨带有小孔的固定绝缘弹性圆筒,圆筒壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径r=0.40m.
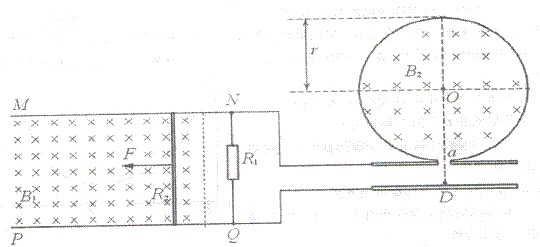
(1)用一个方向平行于MN水平向左且功率P=80W的外力F拉金属杆,使杆从静止开始向左运动.已知杆受到的摩擦阻力大小恒为f=6N,求求当金属杆最终匀速运动时的速度大小;
(2)计算金属杆匀速运动时电容器两极板间的电势差;
(3)当金属杆处于(1)问中的匀速运动状态时,电容器C内紧靠极板D处的一个带正电的粒子加速后从a孔垂直磁场B2并正对着圆心O进入圆筒中,该带电粒子与圆筒壁碰撞两次后恰好又从小孔a射出圆筒.已知该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子的初速度、重力和空气阻力,粒子的荷质比
=5×107 C/kg,求磁感应强度B2的大小.
查看习题详情和答案>>

(1)用一个方向平行于MN水平向左且功率P=80W的外力F拉金属杆,使杆从静止开始向左运动.已知杆受到的摩擦阻力大小恒为f=6N,求求当金属杆最终匀速运动时的速度大小;
(2)计算金属杆匀速运动时电容器两极板间的电势差;
(3)当金属杆处于(1)问中的匀速运动状态时,电容器C内紧靠极板D处的一个带正电的粒子加速后从a孔垂直磁场B2并正对着圆心O进入圆筒中,该带电粒子与圆筒壁碰撞两次后恰好又从小孔a射出圆筒.已知该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子的初速度、重力和空气阻力,粒子的荷质比
| q | m |