摘要:(2)若实验观测到该双星系统中每个星体作匀速圆周运动的实际周期为T观测.且T观测:T计算=1:(N>1).为了解释T观测与T计算的不同.目前有一种流行的理论认为.在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型.我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质.若不考虑其他暗物质的影响.请根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
网址:http://m.1010jiajiao.com/timu_id_1084268[举报]
现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.万有引力常量为G.求:
(1)试计算该双星系统的运动周期T.
(2)若实验上观测到运动周期为T’,且Tn:T=1:
(N>1),为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质--暗物质,作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
查看习题详情和答案>>
(1)试计算该双星系统的运动周期T.
(2)若实验上观测到运动周期为T’,且Tn:T=1:
| N |
现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.万有引力常量为G.求:
(1)试计算该双星系统的运动周期T;
(2)若实验上观测到运动周期为T′,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着密度为ρ的暗物质,而不考虑其它暗物质的影响,并假定暗物质与星体间的相互作用同样遵守万有引力定律.试根据这一模型计算该双星系统的运动周期T′.
查看习题详情和答案>>
(1)试计算该双星系统的运动周期T;
(2)若实验上观测到运动周期为T′,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着密度为ρ的暗物质,而不考虑其它暗物质的影响,并假定暗物质与星体间的相互作用同样遵守万有引力定律.试根据这一模型计算该双星系统的运动周期T′.
现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.万有引力常量为G.求:
(1)试计算该双星系统的运动周期T.
(2)若实验上观测到运动周期为T’,且Tn:T=1:
(N>1),为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质--暗物质,作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
查看习题详情和答案>>
(1)试计算该双星系统的运动周期T.
(2)若实验上观测到运动周期为T’,且Tn:T=1:
| N |
现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距为L,它们正围绕两者连线的中点做圆周运动.
(1)试计算该双星系统的运动周期.
(2)若实验上观测到运动周期为![]() ,且
,且![]() ∶T=1∶
∶T=1∶![]() (N>1).为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质
(N>1).为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质![]() 暗物质.作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
暗物质.作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
用天文望远镜长期观测,人们在宇宙中发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质存在的形式和分布有了较深刻的认识,双星系统是由两个星体构成,其中每个星体的线度都小于两星体间的距离,一般双星系统距离其它星体很远,可以当做孤立系统处理,现根据对某一双星系统的光度学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动。
(1)计算该双星系统的运动周期T计算。
(2)若实验上观测到的运动周期为T观测,且T观测:T计算=1: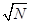 (N>1),为了解释T观测与T计算的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质,作为一种简化模型,我们假定在这两个星体边线为直径的球体内均匀分布着暗物质,而不考虑其它暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
(N>1),为了解释T观测与T计算的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质,作为一种简化模型,我们假定在这两个星体边线为直径的球体内均匀分布着暗物质,而不考虑其它暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
查看习题详情和答案>>