摘要:为了验证地面上的重力与地球吸引月球.太阳吸引行星的力是同一性质的力.遵守同样的规律.牛顿做了著名的“月――地 检验.基本想法是:如果重力和星体间的引力是同一性质的力.都与距离的二次方成反比关系.那么月球绕地球做近似圆周运动的向心加速度和地球表面重力加速度的比值就应该是一个固定的常数.已知月球中心到地球中心的距离是地球半径的60倍.牛顿由此计算出了该常数.证明了他的想法是正确的.请你计算一下.该常数是下列中的哪个?
网址:http://m.1010jiajiao.com/timu_id_1084175[举报]
为了验证地面上的重力、地球吸引月球与太阳吸引行星的力遵循同样的“距离平方反比”规律,牛顿为此做了著名的“月一地”检验.牛顿根据检验的结果,把“距离平方反比”规律推广到自然界中任意两个物体间,发现了具有划时代意义的万有引力定律.
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律.设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R).那么月球绕地球运行的向心加速度an与地面的重力加速度g的比值
=
(用分式表示).
(2)实测数据验算:月球绕地球运行的轨道半径r=3.8×108m,月球运行周期T=27.3天,地面的重力加速度为g=9.8m/s2,由此计算月球绕地球运行的向心加速度a′与地面的重力加速度g的比值
=
(用分式表示).
若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律!
查看习题详情和答案>>
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律.设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R).那么月球绕地球运行的向心加速度an与地面的重力加速度g的比值
| an |
| g |
| 1 |
| 3600 |
| 1 |
| 3600 |
(2)实测数据验算:月球绕地球运行的轨道半径r=3.8×108m,月球运行周期T=27.3天,地面的重力加速度为g=9.8m/s2,由此计算月球绕地球运行的向心加速度a′与地面的重力加速度g的比值
| a′ |
| g |
| 1 |
| 3643 |
| 1 |
| 3643 |
若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律!
为了验证地面上的重力、地球吸引月球与太阳吸引行星的力遵循同样的“距离平方反比”规律,牛顿为此做了著名的“月一地”检验.牛顿根据检验的结果,把“距离平方反比”规律推广到自然界中任意两个物体间,发现了具有划时代意义的万有引力定律.
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律.设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R).那么月球绕地球运行的向心加速度an与地面的重力加速度g的比值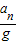 = (用分式表示).
= (用分式表示).
(2)实测数据验算:月球绕地球运行的轨道半径r=3.8×108m,月球运行周期T=27.3天,地面的重力加速度为g=9.8m/s2,由此计算月球绕地球运行的向心加速度a′与地面的重力加速度g的比值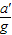 = (用分式表示).
= (用分式表示).
若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律! 查看习题详情和答案>>
“月一地”检验分为两步进行:
(1)理论预期:假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律.设地球半径和月球绕地球运行的轨道半径分别为R和r(已知r=60R).那么月球绕地球运行的向心加速度an与地面的重力加速度g的比值
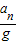 = (用分式表示).
= (用分式表示).(2)实测数据验算:月球绕地球运行的轨道半径r=3.8×108m,月球运行周期T=27.3天,地面的重力加速度为g=9.8m/s2,由此计算月球绕地球运行的向心加速度a′与地面的重力加速度g的比值
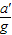 = (用分式表示).
= (用分式表示).若理论预期值与实测数据验算值符合,表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律! 查看习题详情和答案>>
为了验证地面上的物体受到的重力与地球吸引月球、太阳吸引行星的力是同一性质的力,遵守同样的规律,牛顿做过著名的“月-地”检验。基本想法是:如果重力和星体间的引力是同一性质的力,都与距离的二次方成反比关系。由于月心到地心的距离是地球半径的60倍,那么月球绕地球做近似圆周运动的向心加速度应该是地面重力加速度的
[ ]
A.1/3 600
B.3 600倍
C.1/60
D.60倍
查看习题详情和答案>>
B.3 600倍
C.1/60
D.60倍