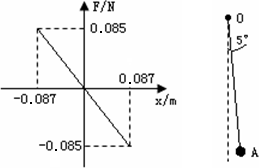
摘要:有一单摆,振动的最大偏角为.如图所示为摆球的回复力与位移的关系图像.摆球的质量为100g.当地的重力加速度为.求:1)摆长和周期,2)摆球的最大速度和最大切向加速度,3) 设向右为正.摆球从A开始振动.画出其振动曲线,4) 当回复力最小时,悬线的拉力大小,
网址:http://m.1010jiajiao.com/timu_id_1082962[举报]
| |||||||||||||||||||||||
| |||||||||||||||||||||||||
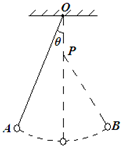 天花板上O点悬挂一单摆,绳子长度为0.99l,质量分布均匀的实心小球质量为m,直径为0.02l,O点正下方0.1l处有一钉子P,如图所示,现将单摆向左拉开一个小角度θ,并由静止释放,小球左右摆动过程中,偏角始终都小于5°,重力加速度为g.求:
天花板上O点悬挂一单摆,绳子长度为0.99l,质量分布均匀的实心小球质量为m,直径为0.02l,O点正下方0.1l处有一钉子P,如图所示,现将单摆向左拉开一个小角度θ,并由静止释放,小球左右摆动过程中,偏角始终都小于5°,重力加速度为g.求:(1)单摆的振动周期;
(2)小球从左摆到最低点时,绳子对小球的拉力大小.
天花板上O点悬挂一单摆,绳子长度为0.99l,质量分布均匀的实心小球质量为m,直径为0.02l,O点正下方0.1l处有一钉子P,如图所示,现将单摆向左拉开一个小角度θ,并由静止释放,小球左右摆动过程中,偏角始终都小于5°,重力加速度为g.求:
(1)单摆的振动周期;
(2)小球从左摆到最低点时,绳子对小球的拉力大小.
查看习题详情和答案>>
(1)单摆的振动周期;
(2)小球从左摆到最低点时,绳子对小球的拉力大小.

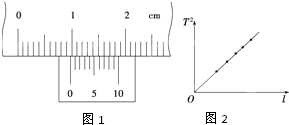
某实验小组在利用单摆测定当地重力加速度的实验中:
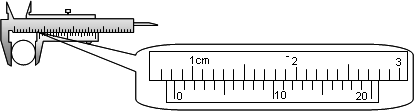
(1)用游标卡尺测定摆球的直径,测量结果如图1所示,则该摆球的直径为 cm.
(2)小组成员在实验过程中有如下说法,其中正确的是 .(填选项前的字母)
A.把单摆从平衡位置拉开30°的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
(3)如果测得的g值偏小,可能的原因是 .
A.测摆线长时摆线拉得过紧
B.摆线上端悬点末固定,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将49次全振动记为50次
(4)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l与T的数据,再以l为横坐标,T2为纵坐标,将所得数据连成直线如图2所示,并求得该直线的斜率为k,则重力加速度g= (用k表示).
查看习题详情和答案>>
(1)用游标卡尺测定摆球的直径,测量结果如图1所示,则该摆球的直径为
(2)小组成员在实验过程中有如下说法,其中正确的是
A.把单摆从平衡位置拉开30°的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
| t | 100 |
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
(3)如果测得的g值偏小,可能的原因是
A.测摆线长时摆线拉得过紧
B.摆线上端悬点末固定,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将49次全振动记为50次
(4)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l与T的数据,再以l为横坐标,T2为纵坐标,将所得数据连成直线如图2所示,并求得该直线的斜率为k,则重力加速度g=