网址:http://m.1010jiajiao.com/timu_id_107105[举报]
11.70 12. 2 13. 14. 【-1,1】 15.(-1,1) 16.
14. 【-1,1】 15.(-1,1) 16. 17.
17.
18、解: (1)由函数 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为 得函数周期为
得函数周期为 ,
,

 直线
直线 是函数
是函数 图像的一条对称轴,
图像的一条对称轴, ,
,
 或
或 ,
, ,
,
 ,
,
 .
.  .
.
(2)

 ,
,
即函数 的单调递增区间为
的单调递增区间为 . ,
. ,
19、解:(1)设公比为q,由题知:2( )=
)= +
+
∴ ,即
,即
∴q=2,即
(2) ,所以
,所以 ①
①
 ②
②
①-②:
∴
 20、解:(Ⅰ) 由题知:
20、解:(Ⅰ) 由题知: ,
,
又∵平面 平面
平面 且交线为
且交线为
∴ 
∴
又∵ ,且
,且
∴ 
(Ⅱ)在平面ABCE内作 .
.
∵平面 平面
平面 且交线为
且交线为
∴  ∴
∴  就是
就是 与平面
与平面 所成角
所成角
由题易求CF=1,DF=5,则
21、解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+
8ax+ 2)(x
2)(x 2)=0
2)=0 x=
x= 或2
或2
∵f(x)有极大值32,而f(2)=0 ∴f( )=
)= ,a=1
,a=1
(2)f/(x)=a(3x 2)(x
2)(x 2)
2)
当a>0时,f(x)=[  2,
2, ]上递增在[
]上递增在[ ]上递减,
]上递减, ,
,
∴0<a<27
当a<0时,f(x)在[ 2,
2, ]上递减,在[
]上递减,在[ ]上递增,f(
]上递增,f( 2)=
2)=

 ,即
,即
∴  综上
综上 
22、解(1)设过抛物线 的焦点
的焦点 的直线方程为
的直线方程为 或
或 (斜率
(斜率 不存在),则
不存在),则  得
得 ,
,
当 (斜率
(斜率 不存在)时,则
不存在)时,则
又
 ,
, 所求抛物线方程为
所求抛物线方程为
(2)设
由已知直线 的斜率分别记为:
的斜率分别记为: ,得
,得




数列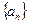 的前n项和记为
的前n项和记为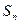 ,前
,前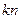 项和记为
项和记为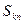
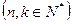 ,对给定的常数
,对给定的常数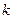 ,若
,若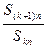 是与
是与 无关的非零常数
无关的非零常数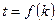 ,则称该数列
,则称该数列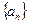 是“
是“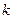 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知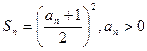 ,求数列
,求数列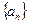 的通项公式(5分);
的通项公式(5分);
(2)、证明(1)的数列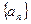 是一个 “
是一个 “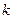 类和科比数列”(4分);
类和科比数列”(4分);
(3)、设正数列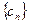 是一个等比数列,首项
是一个等比数列,首项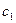 ,公比
,公比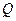
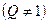 ,若数列
,若数列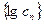 是一个 “
是一个 “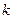 类和科比数列”,探究
类和科比数列”,探究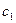 与
与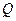 的关系(7分)
的关系(7分)
 的前n项和记为
的前n项和记为 ,
,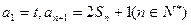
 的前n项和
的前n项和 有最大值,且
有最大值,且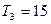 ,又
,又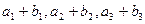 成等比数列,求
成等比数列,求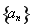
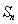

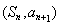
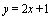

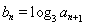


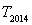
 }的前n项和记为
}的前n项和记为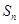 ,a1=t,
,a1=t,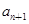 =2
=2 }的前n项和
}的前n项和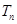 有最大值,且
有最大值,且 =15,又
=15,又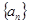 的前n项和记为
的前n项和记为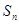 ,前
,前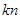 项和记为
项和记为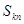
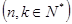 ,对给定的常数
,对给定的常数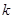 ,若
,若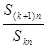 是与
是与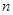 无关的非零常数
无关的非零常数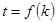 ,则称该数列
,则称该数列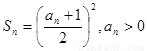 ,求数列
,求数列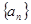 是一个
“
是一个
“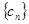 是一个等比数列,首项
是一个等比数列,首项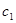 ,公比
,公比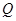
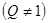 ,若数列
,若数列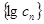 是一个
“
是一个
“