题目内容
数列 的前n项和记为
的前n项和记为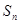 ,前
,前 项和记为
项和记为
 ,对给定的常数
,对给定的常数 ,若
,若 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);
(2)、证明(1)的数列 是一个
“
是一个
“ 类和科比数列”(4分);
类和科比数列”(4分);
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比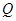
 ,若数列
,若数列 是一个
“
是一个
“ 类和科比数列”,探究
类和科比数列”,探究 与
与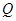 的关系(7分)
的关系(7分)
(1)
(2)
【解析】
理科(1)  作差得
作差得 1分
1分
化简整理 ,
, 2分
2分
所以 成等差数列
1分
成等差数列
1分
计算 1分
1分
 1分
1分
(2)计算 ;
; ;
所以
;
所以 与
与 无关的常数
无关的常数
所以数列 是一个
“
是一个
“ 类和科比数列”
4分
类和科比数列”
4分
(3) 是一个常数,
是一个常数,
所以 是一个等差数列,首项
是一个等差数列,首项 ,公差
,公差 1分
1分

 1分
1分
 1分
1分
 对一切
对一切 恒成立
恒成立
化简整理 对一切
对一切 恒成立
,
恒成立
,
所以 3分
3分
 1分
1分

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案 的前n项和记为
的前n项和记为 ,
,
 的前n项和
的前n项和 有最大值,且
有最大值,且 ,又
,又 成等比数列,求
成等比数列,求









 }的前n项和记为
}的前n项和记为 ,a1=t,
,a1=t, =2
=2 }的前n项和
}的前n项和 有最大值,且
有最大值,且 =15,又
=15,又