摘要：∠ADC=900 .AD//BC.AB⊥AC.AB=AC=2.G为△PAC的重心.E为PB的中点.F在棱BC上且CF=2FB.(4) 求证:FG//平面PAB,(5) 求证:FG⊥AC(6) 当∠PDA多大时.FG⊥平面AEC.
网址：http://m.1010jiajiao.com/timu_id_102365[举报]
在四棱锥P-ABCD中，侧面PCD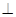
底面ABCD，PD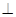CD，底面ABCD是直角梯形，AB∥DC，
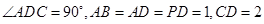ADC-900,AB=AD=PD=1.CD=2.
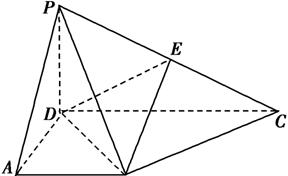
(I)求证：BC平面PBD：
(II)设E为侧棱PC上异于端点的一点，
，试确定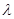
的值，使得二面角
E-BD-P的大小为
．
查看习题详情和答案>>
在四棱锥P-ABCD中，侧面PCD
底面ABCD，
PDCD，底面ABCD是直角梯形，AB∥DC，
ADC -900,AB= AD= PD=1.CD=2.
(I)求证：BC平面PBD：
(II)设E为侧棱PC上异于端点的一点，
，试确定
的值，使得二面角
E-BD -P的大小为
．
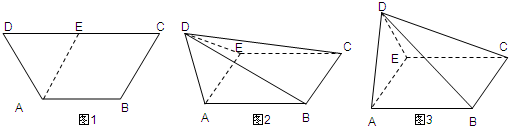如图1，等腰梯形ABCD中，AB=2，CD=4，∠ADC=∠BCD=60°．取线段CD中点E，将△ADE沿AE折起，如图2所示．（1）当平面ADE折到与底面ABCE所成的二面角为900时，如图3所示，求此时二面角A-BD-C平面角的余弦值．
（2）在将△ADE开始折起到与△ABE重合的过程中，求直线DC与平面ABCE所成角的正切值的取值范围． 查看习题详情和答案>>
中，AD//BC, 
=900，BA="BC"
把ΔBAC沿
折起到
的位置,使得点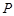
在平面ADC上的正投影O恰好落在线段
分别为线段PC，CD的中点．
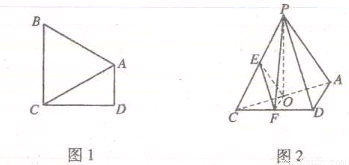
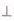与平面POF
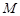,使得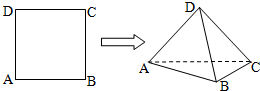
如图，已知正方形ABCD的边长为2，沿对角线AC将三角形ADC折起，使平面ADC与平面ABC垂直，折叠后B、D两点的距离是（ ）