摘要：∴存在常数c∈(0,7-4)∪(7+4,+∞).使H(x)在内有极值点.点评:导数的加盟.大大拓展了命制函数类探索题的空间.从两个样题来看.函数类的探索题的解决离不开函数的主体知识.因此夯实函数“三基 就可以以不变应万变.
网址：http://m.1010jiajiao.com/timu_id_102223[举报]
已知等差数列{an}中，公差d＞0，其前n项和为Sn，且满足a2•a3=45，a1+a4=14．
（1）求数列{an}的通项公式；
（2）设bn=
（n∈N*），数列{bn}的前n项和为Tn，求证：
≤Tn＜1；
（3）是否存在常数c（c≠0），使得数列{
}为等差数列？若存在，试求出c；若不存在，说明理由．
查看习题详情和答案>>
（1）求数列{an}的通项公式；
（2）设bn=
| 4 |
| n•(an+7) |
| 1 |
| 2 |
（3）是否存在常数c（c≠0），使得数列{
| Sn |
| n+c |
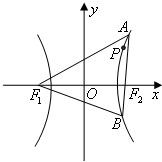设动点P到点F1（-1，0）和F2（1，0）的距离分别为d1和d2，∠F1PF2=2θ，且存在常数λ（0＜λ＜1），使得d1d2sin2θ=λ．（1）证明：动点P的轨迹C为双曲线，并求出C的方程；
（2）如图，过点F2的直线与双曲线C的右支交于A，B两点．问：是否存在λ，使△F1AB是以点B为直角顶点的等腰直角三角形？若存在，求出λ的值；若不存在，说明理由． 查看习题详情和答案>>
（2013•南通三模）设f（x）是定义在（0，+∞）的可导函数，且不恒为0，记gn(x)=
(n∈N*)．若对定义域内的每一个x，总有gn（x）＜0，则称f（x）为“n阶负函数”；若对定义域内的每一个x，总有[gn(x)]′≥0，则称f（x）为“n阶不减函数”（[gn(x)]′为函数gn（x）的导函数）．
（1）若f(x)=
-
-x(x＞0)既是“1阶负函数”，又是“1阶不减函数”，求实数a的取值范围；
（2）对任给的“2阶不减函数”f（x），如果存在常数c，使得f（x）＜c恒成立，试判断f（x）是否为“2阶负函数”？并说明理由．
查看习题详情和答案>>
| f(x) |
| xn |
（1）若f(x)=
| a |
| x3 |
| 1 |
| x |
（2）对任给的“2阶不减函数”f（x），如果存在常数c，使得f（x）＜c恒成立，试判断f（x）是否为“2阶负函数”？并说明理由．