题目内容
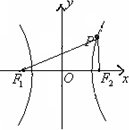
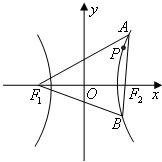 设动点P到点F1(-1,0)和F2(1,0)的距离分别为d1和d2,∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
设动点P到点F1(-1,0)和F2(1,0)的距离分别为d1和d2,∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
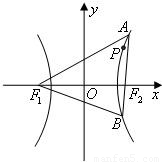
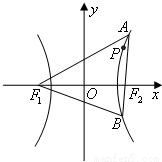
(2)如图,过点F2的直线与双曲线C的右支交于A,B两点.问:是否存在λ,使△F1AB是以点B为直角顶点的等腰直角三角形?若存在,求出λ的值;若不存在,说明理由.
分析:(1)在△PF1F2中,利用余弦定理得出d1-d2是一个常数,从而动点P的轨迹C是以F1,F2为焦点的双曲线,最后求出双曲线的方程即可;
(2)在△AF1B中,设|AF1|=d1,|AF2|=d2,|BF1|=d3,|BF2|=d4.对于存在性问题,可先假设存在,即假设△AF1B为等腰直角三角形,再利用方程组,求出λ的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(2)在△AF1B中,设|AF1|=d1,|AF2|=d2,|BF1|=d3,|BF2|=d4.对于存在性问题,可先假设存在,即假设△AF1B为等腰直角三角形,再利用方程组,求出λ的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)在△PF1F2中,
|F1F2|=24=d12+d22-2d1d2cos2θ=(d1-d2)2+4d1d2sin2θ
(d1-d2)2=4-4λ
∴|d1-d2|=2
(小于2的常数)
故动点P的轨迹C是以F1,F2为焦点,实轴长2a=2
的双曲线.
方程为
-
=1.
(2)在△AF1B中,设|AF1|=d1,|AF2|=d2,|BF1|=d3,|BF2|=d4.
假设△AF1B为等腰直角三角形,则
由②与③得d2=2a,
则
由⑤得d3d4=2λ,4
(
-1)a2=2λ,(8-4
)(1-λ)=2λ,λ=
∈(0,1)
故存在λ=
满足题设条件.
|F1F2|=24=d12+d22-2d1d2cos2θ=(d1-d2)2+4d1d2sin2θ
(d1-d2)2=4-4λ
∴|d1-d2|=2
| 1-λ |
故动点P的轨迹C是以F1,F2为焦点,实轴长2a=2
| 1-λ |
方程为
| x2 |
| 1-λ |
| y2 |
| λ |
(2)在△AF1B中,设|AF1|=d1,|AF2|=d2,|BF1|=d3,|BF2|=d4.
假设△AF1B为等腰直角三角形,则
|
由②与③得d2=2a,
则
|
由⑤得d3d4=2λ,4
| 2 |
| 2 |
| 2 |
12-2
| ||
| 17 |
故存在λ=
12-2
| ||
| 17 |
点评:本小题主要考查直线与圆锥曲线的综合问题、直线的方程、双曲线方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目