网址:http://m.1010jiajiao.com/timu_id_102149[举报]
设函数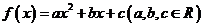 ,若
,若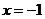 为函数
为函数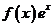 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为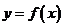 的图象是
的图象是
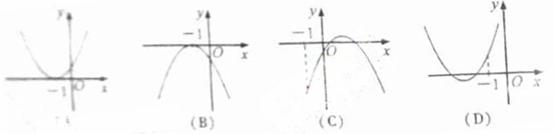
【答案】D
【解析】设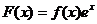 ,∴
,∴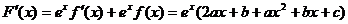 ,
,
又∴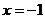 为
为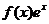 的一个极值点,
的一个极值点,
∴ ,即
,即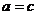 ,
,
∴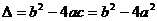 ,
,
当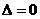 时,
时,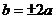 ,即对称轴所在直线方程为
,即对称轴所在直线方程为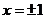 ;
;
当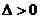 时,
时,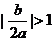 ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.
查看习题详情和答案>>
如图,直线 与抛物线
与抛物线 交于
交于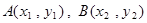 两点,与
两点,与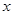 轴相交于点
轴相交于点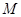 ,且
,且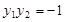 .
.
(1)求证: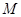 点的坐标为
点的坐标为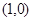 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为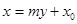 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据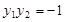 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
查看习题详情和答案>>
设抛物线 :
: (
( >0)的焦点为
>0)的焦点为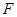 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以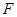 为圆心,
为圆心,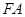 为半径的圆
为半径的圆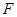 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为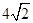 ,求
,求 的值及圆
的值及圆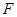 的方程;
的方程;
(Ⅱ)若 ,
, ,
,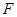 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
=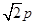 ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|=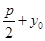 ,
,
∵ 的面积为
的面积为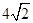 ,∴
,∴ =
= =
= =
=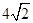 ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
,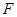 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆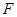 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: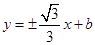 ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
=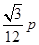 ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点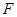 对称得:
对称得: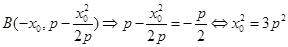
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
查看习题详情和答案>>
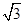 ,2) (B)(0,2)
(C)(
,2) (B)(0,2)
(C)( ,由图象可知当直线
,由图象可知当直线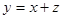 经过点B时,截距最大,此时
经过点B时,截距最大,此时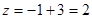 ,当直线经过点C时,直线截距最小.因为
,当直线经过点C时,直线截距最小.因为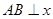 轴,所以
轴,所以 ,三角形的边长为2,设
,三角形的边长为2,设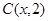 ,则
,则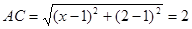 ,解得
,解得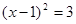 ,
,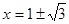 ,因为顶点C在第一象限,所以
,因为顶点C在第一象限,所以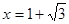 ,即
,即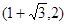 代入直线
代入直线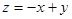 得
得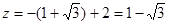 ,所以
,所以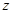 的取值范围是
的取值范围是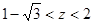 ,选A.
,选A.