35.(供选1)某同学在做“描绘小电珠的伏安特性曲线”的实验中得到如下一组U和I的数据:
|
编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
U(伏) |
0.20 |
0.60 |
1.00 |
1.40 |
1.80 |
2.20 |
2.60 |
3.00 |
|
I(安) |
0.020 |
0.060 |
0.100 |
0.140 |
0.170 |
0.190 |
0.200 |
0.205 |
|
灯泡发光情况 |
不亮 微亮 逐渐变亮 正常发光 |
①在下面的方框中画出实验电路图:
②在右图上画出I-U图线.
 ③从图线上可以看出,当功率逐渐增大时,灯丝电阻的变化情况是
.
③从图线上可以看出,当功率逐渐增大时,灯丝电阻的变化情况是
.
④这表明导体的电阻随温度升高而

(供选2)
为了描绘一个“6V、3W”小灯泡的伏安特性曲线,有下列器材:
A、伏特表(量程0--15V,内阻1.5KΩ),B、伏特表(量程0--9V,内阻4KΩ)
C、安培表(量程0--0.6A,内阻0.5Ω),D、安培表(量程0--3A,内阻0.1Ω)
E、滑动变阻器:(0--20Ω、1A),F、滑动变阻器:(0--200Ω、0.1A)
G、蓄电池:(4V,内阻不计),H、蓄电池:(12V,内阻不计)
问:安培表应选 C ,伏特表选 B ,滑动变阻器用 E ,电源用 H。
(2)实验电路图应选下图中 C 较为合理。




 (3)所描绘的伏安特性曲线的大致形状为下图中的哪个? B 。
(3)所描绘的伏安特性曲线的大致形状为下图中的哪个? B 。

34.某同学在探究影响单摆振动周期的因素时,针对自己考虑到的几个可能影响周期的物理量设计了实验方案,并认真进行了实验操作,取得了实验数据.他经过分析后,在实验误差范围内,找到了在摆角较小的情况下影响单摆周期的一个物理量,并通过作图象找到了单摆周期与这个物理量的明确的数量关系.该同学的实验数据记录如下.
 质量m /g |
0.700 |
0.750 |
0.800 |
0.850 |
0.900 |
|
|
钢球A 8.0 |
3.0 |
1.69 |
1.73 |
1.80 |
1.86 |
1.89 |
|
9.0 |
1.68 |
1.74 |
1.79 |
1.85 |
1.90 |
|
|
钢球B 16.0 |
3.0 |
1.68 |
1.74 |
1.79 |
1.85 |
1.90 |
|
9.0 |
1.69 |
1.73 |
1.80 |
1.85 |
1.89 |
|
|
铜球 20.0 |
3.0 |
1.68 |
1.74 |
1.80 |
1.85 |
1.90 |
|
9.0 |
1.68 |
1.74 |
1.79 |
1.85 |
1.90 |
|
|
铝球 6.0 |
3.0 |
1.68 |
1.74 |
1.80 |
1.85 |
1.90 |
|
9.0 |
1.69 |
1.74 |
1.80 |
1.86 |
1.91 |
(1) 分析上面实验表格中的数据,你认为在摆角较小的情况下影响单摆周期的这个物理量是: .
(2) 利用表中给出的数据,在图7给出的坐标图上画出一条能明确确定单摆周期与这个物理量关系的图线,由此可见单摆周期与这个物理量的数学关系是 .


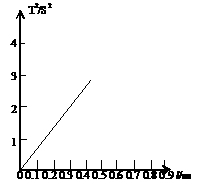 (1)摆长l。
(1)摆长l。
(2)T2=kl
 (弹簧的形变在弹性限度内),则木块A所受重力的大小等于
(弹簧的形变在弹性限度内),则木块A所受重力的大小等于 C.
C. D.
D.
 1831年发现电磁感应现象的物理学家是
1831年发现电磁感应现象的物理学家是 (供选1)如图所示,在置于匀强磁场中的平行金属导轨上,横跨在两导轨间的导体杆MN以v=2m/s速度向右移动,已知磁感应强度B=0.5T,方向垂直于导轨平面(纸面)向外,导轨间距离为l=0.6m,电阻R=1.8Ω,导体杆电阻r=0.2Ω,导轨电阻不计。求:
(供选1)如图所示,在置于匀强磁场中的平行金属导轨上,横跨在两导轨间的导体杆MN以v=2m/s速度向右移动,已知磁感应强度B=0.5T,方向垂直于导轨平面(纸面)向外,导轨间距离为l=0.6m,电阻R=1.8Ω,导体杆电阻r=0.2Ω,导轨电阻不计。求: 时,水平拉力的功率;
时,水平拉力的功率;
 可知,此时杆中的感应电流也最大.
可知,此时杆中的感应电流也最大.  m/s时,电流为最大值的
m/s时,电流为最大值的 ,即
,即  A
A N,方向水平向左
N,方向水平向左 = 7.5×10-2 W
= 7.5×10-2 W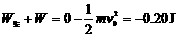
 = -7.0×10-2 J
= -7.0×10-2 J (1)匀强电场的电场强度E的大小;
(1)匀强电场的电场强度E的大小; N/C = 2.0×104 N/C
N/C = 2.0×104 N/C (供选2)一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,AB与电场线的夹角为α,已知带电微粒的质量为m,带电量为q,A、B相距L。则
(供选2)一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,AB与电场线的夹角为α,已知带电微粒的质量为m,带电量为q,A、B相距L。则
 ,电池组的电动势
,电池组的电动势 ,内电阻
,内电阻 .求:开关S闭合后通过电阻R的电流和电阻R消耗的电功率.
.求:开关S闭合后通过电阻R的电流和电阻R消耗的电功率.
 (1)物体加速度a的大小;
(1)物体加速度a的大小; =
=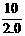 m/s2 = 5.0 m/s2
m/s2 = 5.0 m/s2
 ×5.0×2.02 m = 10 m
×5.0×2.02 m = 10 m
