15.
(8分)解:设过桥前减速过程所需时间为t1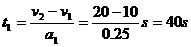 ………………2分
………………2分设过桥所用的时间为t2. 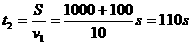 ………………2分 ………………2分设过桥后加速度过程所需时间为t3 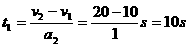 ………………2分 ………………2分共用时间  ………………2分 ………………2分 |
116、(8分)解析:作出小球1的受力示意图并合成两弹力如右图, 因为OA=OB,且∠AOB=60º,所以△AOB为等边三角形,又F的方向与OB垂直,故F的方向沿∠OAB的角平分线方向。 根据平衡条件和几何知识得: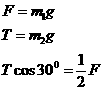
解得: 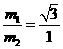 评分标准 每式2分 |
17(8分)解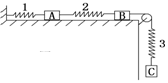 解:(1)对C物体由平衡条件得:F3=mcg=30N 1分 解:(1)对C物体由平衡条件得:F3=mcg=30N 1分由胡克定律 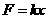 得:F1=0 1分 得:F1=0 1分由 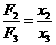 得:F2=20N
2分 得:F2=20N
2分(2)对A物体由平衡条件得: 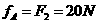 ,水平向左。 2分 ,水平向左。 2分(3)对B物体由平衡条件得: 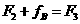 得: 得: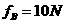 ,水平向左。 2分 ,水平向左。 2分 |
|
18(10分)解 (1)小球通过P 物体的平均时间: t =(0.019 + 0.020 + 0.021 + 0.021 + 0.019)/5 = 0.020s 1 分 由已知可知小球刚到达P 的顶端的速度: V1 = h/t = 1.2/0.020 = 60m/s 2 分 则楼顶距P 物体顶端的距离: 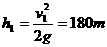 2
分 2
分(2)由(1)可知,设小球到达物体P 顶端速度为v2,则: 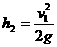 2 分 2 分设下抛初速度为v0,则: 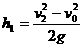 2
分 2
分由以上两式可得: 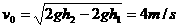 1
分 1
分 |
|
19(9分)解 (1)以两个正方体整体为研究对象 整体受到向上的支持力和向下的重力,整全处于静止状态 ………2分 所以水平面对正方体M的弹力大小为(M+m)g………………..2分 (2)对正方体m进行受力分析如图 …..1分 把N2沿水平方向和竖直方向分解 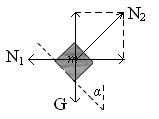 有 有 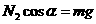 ……………………..1分 ……………………..1分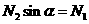 …………………………1分 …………………………1分解得  ………………………..2分 ………………………..2分 |
|
20(12分) 解:(1)设摩托车与某一辆汽车速度相同时需要时间t 则有V1=V2-at-----(1分) 得:t=20s -----(1分) 在此段时间内摩托车前行距离 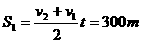 ----(1分) ----(1分)汽车前行距离S2=V1 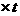 =200m
(1分) =200m
(1分)摩托车相遇的汽车数为N= 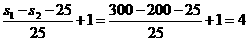 辆---(1分) 辆---(1分)最多相遇 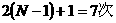 ----(1分) ----(1分)(2)设摩托车与相距最近的汽车相遇需要的时间为t 则有位移关系: 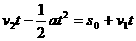 ---(2分) ---(2分) 代入数据,化简得: 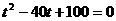 解得: 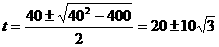 s-------(1分) s-------(1分)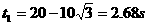 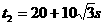 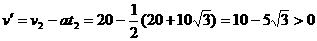 ---(1分) ---(1分)即摩托车离开车队时,摩托车没有停止---(1分) 两车相遇经历的时间 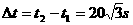 =34.6s----(1分) =34.6s----(1分) |
18.(10分)甲乙两位同学在一次做”测量高楼的高度”的研究性课题中,设计了以下一个方案: 由甲同学在楼顶静止释放一个小球,乙同学通过数字计时器装置,测出小球通过放置在地面上高为1.2m 物体P 的时间, 从而估算出楼高,假设该方法在实践中能成功(由于小球在经过物体P 过程中,速度的变化和它的瞬时速度相比较,可以忽略不计,因而可以看成是匀速直线运动)(g 取10m/s2)。
|
次数 |
1 |
2 |
3 |
4 |
5 |
|
时间/s |
0.019 |
0.020 |
0.021 |
0.021 |
0.019 |
(1)乙同学测得其中5 次的试验数据如上表,试估算该高楼楼顶到物体P 顶端的距离。
(2)在某次试验中,甲同学以某一初速度竖直向下抛小球,乙同学仍以为甲同学是静止释放小球的,结果计算出高楼楼顶到物体P 顶端的距离大约是180.8m,试求出甲同学这次抛出小球的初速度的大小。
 gt2(3分)
gt2(3分)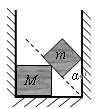 (9分)如图所示,质量为m的正方体和质量为M的正方体放在两竖直墙和水平面问,处于静止状态。m与M相接触边与竖直方向的夹角为α若不计一切摩擦,
(9分)如图所示,质量为m的正方体和质量为M的正方体放在两竖直墙和水平面问,处于静止状态。m与M相接触边与竖直方向的夹角为α若不计一切摩擦,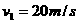 的正常速度行驶,当通过1000m长的大桥时,必须以v2=10m/s的速度行驶。在列车上桥前需提前减速,当列车头刚上桥时速度恰好为10m/s;列车全部离开大桥时又需通过加速恢复原来的速度。减速过程中,加速度大小为0.25m/s2。加速过程中,加速度大小为1m/s2,则该列车从减速开始算起,到过桥后速度达到20m/s,共用了多长时间?
的正常速度行驶,当通过1000m长的大桥时,必须以v2=10m/s的速度行驶。在列车上桥前需提前减速,当列车头刚上桥时速度恰好为10m/s;列车全部离开大桥时又需通过加速恢复原来的速度。减速过程中,加速度大小为0.25m/s2。加速过程中,加速度大小为1m/s2,则该列车从减速开始算起,到过桥后速度达到20m/s,共用了多长时间?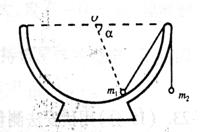 16(8分)一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和 m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。求两小球的质量之比
16(8分)一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和 m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。求两小球的质量之比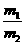 。
。

 00
00